---
id: 5900f5021000cf542c510014
title: 'Problema 405: Colocação retangular de ladrilhos'
challengeType: 5
forumTopicId: 302073
dashedName: problem-405-a-rectangular-tiling
---
# --description--
Queremos preencher com ladrilhos um retângulo cujo comprimento é o dobro de sua largura.
Considere $T(0)$ como a área a ser ladrilhada, consistindo em um único retângulo.
Para $n > 0$, considere $T(n)$ como tendo sido obtido a partir de $T( n- 1)$ substituindo todos os ladrilhos da seguinte maneira:
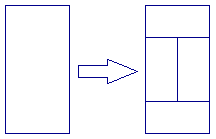A animação a seguir demonstra o preenchimento com ladrilhos de $T(n)$ para $n$ de 0 a 5:
Considere $f(n)$ como o número de pontos em que quatro ladrilhos se encontram em $T(n)$. Por exemplo, $f(1) = 0$, $f(4) = 82$ e $f({10}^9)\bmod {17}^7 = 126.897.180$.
Encontre $f({10}^k)$ para $k = {10}^{18}$ e dê sua resposta modulo ${17}^7$.
# --hints--
`rectangularTiling()` deve retornar `237696125`.
```js
assert.strictEqual(rectangularTiling(), 237696125);
```
# --seed--
## --seed-contents--
```js
function rectangularTiling() {
return true;
}
rectangularTiling();
```
# --solutions--
```js
// solution required
```