---
id: 5900f5081000cf542c51001a
title: 'Problema 412: Númeração de Gnomon'
challengeType: 5
forumTopicId: 302081
dashedName: problem-412-gnomon-numbering
---
# --description--
Para números inteiros $m$, $n$ ($0 ≤ n < m$), considere $L(m, n)$ como uma grade $m×m$ grid com a parte superior direita $n×n$ da grade removida.
Por exemplo, $L(5, 3)$ terá essa aparência:
 Queremos numerar cada célula de $L(m, n)$ com números inteiros consecutivos 1, 2, 3, ... tal que o número em cada célula seja menor que o número abaixo e à esquerda dele.
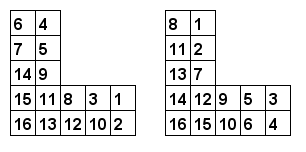
Por exemplo, aqui temos duas numerações válidas de $L(5, 3)$:
Queremos numerar cada célula de $L(m, n)$ com números inteiros consecutivos 1, 2, 3, ... tal que o número em cada célula seja menor que o número abaixo e à esquerda dele.
Por exemplo, aqui temos duas numerações válidas de $L(5, 3)$:
 Considere $LC(m, n)$ como a quantidade de numerações válidas de $L(m, n)$. Pode-se verificar que $LC(3, 0) = 42$, $LC(5, 3) = 250.250$, $LC(6, 3) = 406.029.023.400$ e $LC(10, 5)\bmod 76.543.217 = 61.251.715$.
Encontre $LC(10.000, 5.000)\bmod 76.543.217$.
# --hints--
`gnomonNumbering()` deve retornar `38788800`.
```js
assert.strictEqual(gnomonNumbering(), 38788800);
```
# --seed--
## --seed-contents--
```js
function gnomonNumbering() {
return true;
}
gnomonNumbering();
```
# --solutions--
```js
// solution required
```
Considere $LC(m, n)$ como a quantidade de numerações válidas de $L(m, n)$. Pode-se verificar que $LC(3, 0) = 42$, $LC(5, 3) = 250.250$, $LC(6, 3) = 406.029.023.400$ e $LC(10, 5)\bmod 76.543.217 = 61.251.715$.
Encontre $LC(10.000, 5.000)\bmod 76.543.217$.
# --hints--
`gnomonNumbering()` deve retornar `38788800`.
```js
assert.strictEqual(gnomonNumbering(), 38788800);
```
# --seed--
## --seed-contents--
```js
function gnomonNumbering() {
return true;
}
gnomonNumbering();
```
# --solutions--
```js
// solution required
```
 Queremos numerar cada célula de $L(m, n)$ com números inteiros consecutivos 1, 2, 3, ... tal que o número em cada célula seja menor que o número abaixo e à esquerda dele.
Por exemplo, aqui temos duas numerações válidas de $L(5, 3)$:
Queremos numerar cada célula de $L(m, n)$ com números inteiros consecutivos 1, 2, 3, ... tal que o número em cada célula seja menor que o número abaixo e à esquerda dele.
Por exemplo, aqui temos duas numerações válidas de $L(5, 3)$:
 Considere $LC(m, n)$ como a quantidade de numerações válidas de $L(m, n)$. Pode-se verificar que $LC(3, 0) = 42$, $LC(5, 3) = 250.250$, $LC(6, 3) = 406.029.023.400$ e $LC(10, 5)\bmod 76.543.217 = 61.251.715$.
Encontre $LC(10.000, 5.000)\bmod 76.543.217$.
# --hints--
`gnomonNumbering()` deve retornar `38788800`.
```js
assert.strictEqual(gnomonNumbering(), 38788800);
```
# --seed--
## --seed-contents--
```js
function gnomonNumbering() {
return true;
}
gnomonNumbering();
```
# --solutions--
```js
// solution required
```
Considere $LC(m, n)$ como a quantidade de numerações válidas de $L(m, n)$. Pode-se verificar que $LC(3, 0) = 42$, $LC(5, 3) = 250.250$, $LC(6, 3) = 406.029.023.400$ e $LC(10, 5)\bmod 76.543.217 = 61.251.715$.
Encontre $LC(10.000, 5.000)\bmod 76.543.217$.
# --hints--
`gnomonNumbering()` deve retornar `38788800`.
```js
assert.strictEqual(gnomonNumbering(), 38788800);
```
# --seed--
## --seed-contents--
```js
function gnomonNumbering() {
return true;
}
gnomonNumbering();
```
# --solutions--
```js
// solution required
```