---
id: 5900f51f1000cf542c510031
title: 'Problema 434: Grafos rígidos'
challengeType: 5
forumTopicId: 302105
dashedName: problem-434-rigid-graphs
---
# --description--
Lembre-se de que um grafo é uma coleção de vértices e bordas conectando os vértices, e que dois vértices conectados por uma aresta são chamados de adjacentes.
Grafos podem ser incorporados no espaço euclideano associando cada vértice com um ponto nesse espaço.
Um grafo flexível é uma incorporação de um grafo no qual é possível mover um ou mais vértices continuamente para que a distância entre pelo menos dois vértices não adjacentes seja alterada enquanto as distâncias entre cada par de vértices adjacentes seja mantida constante.
Um grafo rígido é uma incorporação de um grafo que não é flexível.
Informalmente, um grafo é rígido se, ao substituir os vértices por dobradiças de rotação completa e as arestas por hastes não elásticas e não curvas, nenhuma parte do grafo poderá se mover de modo independente do resto do grafo.
Os grafos de grade incorporados no plano euclideano não são rígidos, como demonstra a animação a seguir:
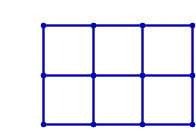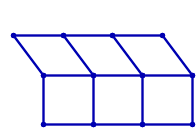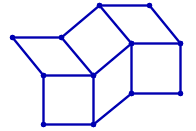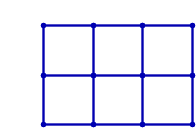 No entanto, é possível torná-los rígidos adicionando arestas diagonais às células. Por exemplo, para o grafo de grade 2x3, há 19 maneiras de tornar o grafo rígido:
No entanto, é possível torná-los rígidos adicionando arestas diagonais às células. Por exemplo, para o grafo de grade 2x3, há 19 maneiras de tornar o grafo rígido:
 Observe que, para fins deste problema, não consideramos a troca da orientação de uma aresta diagonal nem adicionar arestas diagonais a uma célula como uma forma diferente de fazer um grafo de grade rígido.
Considere $R(m, n)$ como o número de maneiras de tornar um grafo de grade $m × n$ rígido.
Ex: $R(2, 3) = 19$ e $R(5, 5) = 23.679.901$.
Defina $S(N)$ como $\sum R(i, j)$ para $1 ≤ i$, $j ≤ N$.
Ex: $S(5) = 25.021.721$.
Encontre $S(100)$, dê sua resposta modulo $1.000.000.033$.
# --hints--
`rigidGraphs()` deve retornar `863253606`.
```js
assert.strictEqual(rigidGraphs(), 863253606);
```
# --seed--
## --seed-contents--
```js
function rigidGraphs() {
return true;
}
rigidGraphs();
```
# --solutions--
```js
// solution required
```
Observe que, para fins deste problema, não consideramos a troca da orientação de uma aresta diagonal nem adicionar arestas diagonais a uma célula como uma forma diferente de fazer um grafo de grade rígido.
Considere $R(m, n)$ como o número de maneiras de tornar um grafo de grade $m × n$ rígido.
Ex: $R(2, 3) = 19$ e $R(5, 5) = 23.679.901$.
Defina $S(N)$ como $\sum R(i, j)$ para $1 ≤ i$, $j ≤ N$.
Ex: $S(5) = 25.021.721$.
Encontre $S(100)$, dê sua resposta modulo $1.000.000.033$.
# --hints--
`rigidGraphs()` deve retornar `863253606`.
```js
assert.strictEqual(rigidGraphs(), 863253606);
```
# --seed--
## --seed-contents--
```js
function rigidGraphs() {
return true;
}
rigidGraphs();
```
# --solutions--
```js
// solution required
```
 No entanto, é possível torná-los rígidos adicionando arestas diagonais às células. Por exemplo, para o grafo de grade 2x3, há 19 maneiras de tornar o grafo rígido:
No entanto, é possível torná-los rígidos adicionando arestas diagonais às células. Por exemplo, para o grafo de grade 2x3, há 19 maneiras de tornar o grafo rígido:
 Observe que, para fins deste problema, não consideramos a troca da orientação de uma aresta diagonal nem adicionar arestas diagonais a uma célula como uma forma diferente de fazer um grafo de grade rígido.
Considere $R(m, n)$ como o número de maneiras de tornar um grafo de grade $m × n$ rígido.
Ex: $R(2, 3) = 19$ e $R(5, 5) = 23.679.901$.
Defina $S(N)$ como $\sum R(i, j)$ para $1 ≤ i$, $j ≤ N$.
Ex: $S(5) = 25.021.721$.
Encontre $S(100)$, dê sua resposta modulo $1.000.000.033$.
# --hints--
`rigidGraphs()` deve retornar `863253606`.
```js
assert.strictEqual(rigidGraphs(), 863253606);
```
# --seed--
## --seed-contents--
```js
function rigidGraphs() {
return true;
}
rigidGraphs();
```
# --solutions--
```js
// solution required
```
Observe que, para fins deste problema, não consideramos a troca da orientação de uma aresta diagonal nem adicionar arestas diagonais a uma célula como uma forma diferente de fazer um grafo de grade rígido.
Considere $R(m, n)$ como o número de maneiras de tornar um grafo de grade $m × n$ rígido.
Ex: $R(2, 3) = 19$ e $R(5, 5) = 23.679.901$.
Defina $S(N)$ como $\sum R(i, j)$ para $1 ≤ i$, $j ≤ N$.
Ex: $S(5) = 25.021.721$.
Encontre $S(100)$, dê sua resposta modulo $1.000.000.033$.
# --hints--
`rigidGraphs()` deve retornar `863253606`.
```js
assert.strictEqual(rigidGraphs(), 863253606);
```
# --seed--
## --seed-contents--
```js
function rigidGraphs() {
return true;
}
rigidGraphs();
```
# --solutions--
```js
// solution required
```