---
id: 5900f4ee1000cf542c510000
title: 'Завдання 385: Еліпси всередині трикутників'
challengeType: 5
forumTopicId: 302049
dashedName: problem-385-ellipses-inside-triangles
---
# --description--
На площині будь-якого трикутника $T$ можна зобразити унікальний еліпс, який повністю розташовується всередині $T$.
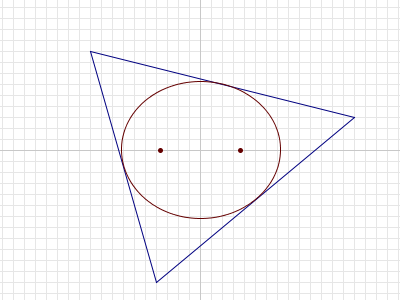 Для даного $n$ розглянемо такі трикутники $T$:
- вершини $T$ мають цілі координати з абсолютним значенням $≤ n$
- $(\sqrt{13}, 0)$ та $(-\sqrt{13}, 0)$ є фокусами1 найбільшого еліпса в межах $T$.
Нехай $A(n)$ — це сума площ усіх таких трикутників.
Наприклад, якщо $n = 8$, то є два таких трикутників. Їхні вершини: (-4,-3), (-4,3), (8,0) та (4,3), (4,-3), (-8,0), а площа кожного трикутника — 36. Таким чином $A(8) = 36 + 36 = 72$.
Можна перевірити, що $A(10) = 252$, $A(100) = 34\\,632$ та $A(1000) = 3\\,529\\,008$.
Знайдіть $A(1\\,000\\,000\\,000)$.
1Фокусами еліпса є дві точки $A$ та $B$. Для кожної точки $P$ на межі еліпса $AP + PB$ є константою.
# --hints--
`ellipsesInsideTriangles()` має повернути `3776957309612154000`.
```js
assert.strictEqual(ellipsesInsideTriangles(), 3776957309612154000);
```
# --seed--
## --seed-contents--
```js
function ellipsesInsideTriangles() {
return true;
}
ellipsesInsideTriangles();
```
# --solutions--
```js
// solution required
```
Для даного $n$ розглянемо такі трикутники $T$:
- вершини $T$ мають цілі координати з абсолютним значенням $≤ n$
- $(\sqrt{13}, 0)$ та $(-\sqrt{13}, 0)$ є фокусами1 найбільшого еліпса в межах $T$.
Нехай $A(n)$ — це сума площ усіх таких трикутників.
Наприклад, якщо $n = 8$, то є два таких трикутників. Їхні вершини: (-4,-3), (-4,3), (8,0) та (4,3), (4,-3), (-8,0), а площа кожного трикутника — 36. Таким чином $A(8) = 36 + 36 = 72$.
Можна перевірити, що $A(10) = 252$, $A(100) = 34\\,632$ та $A(1000) = 3\\,529\\,008$.
Знайдіть $A(1\\,000\\,000\\,000)$.
1Фокусами еліпса є дві точки $A$ та $B$. Для кожної точки $P$ на межі еліпса $AP + PB$ є константою.
# --hints--
`ellipsesInsideTriangles()` має повернути `3776957309612154000`.
```js
assert.strictEqual(ellipsesInsideTriangles(), 3776957309612154000);
```
# --seed--
## --seed-contents--
```js
function ellipsesInsideTriangles() {
return true;
}
ellipsesInsideTriangles();
```
# --solutions--
```js
// solution required
```
 Для даного $n$ розглянемо такі трикутники $T$:
- вершини $T$ мають цілі координати з абсолютним значенням $≤ n$
- $(\sqrt{13}, 0)$ та $(-\sqrt{13}, 0)$ є фокусами1 найбільшого еліпса в межах $T$.
Нехай $A(n)$ — це сума площ усіх таких трикутників.
Наприклад, якщо $n = 8$, то є два таких трикутників. Їхні вершини: (-4,-3), (-4,3), (8,0) та (4,3), (4,-3), (-8,0), а площа кожного трикутника — 36. Таким чином $A(8) = 36 + 36 = 72$.
Можна перевірити, що $A(10) = 252$, $A(100) = 34\\,632$ та $A(1000) = 3\\,529\\,008$.
Знайдіть $A(1\\,000\\,000\\,000)$.
1Фокусами еліпса є дві точки $A$ та $B$. Для кожної точки $P$ на межі еліпса $AP + PB$ є константою.
# --hints--
`ellipsesInsideTriangles()` має повернути `3776957309612154000`.
```js
assert.strictEqual(ellipsesInsideTriangles(), 3776957309612154000);
```
# --seed--
## --seed-contents--
```js
function ellipsesInsideTriangles() {
return true;
}
ellipsesInsideTriangles();
```
# --solutions--
```js
// solution required
```
Для даного $n$ розглянемо такі трикутники $T$:
- вершини $T$ мають цілі координати з абсолютним значенням $≤ n$
- $(\sqrt{13}, 0)$ та $(-\sqrt{13}, 0)$ є фокусами1 найбільшого еліпса в межах $T$.
Нехай $A(n)$ — це сума площ усіх таких трикутників.
Наприклад, якщо $n = 8$, то є два таких трикутників. Їхні вершини: (-4,-3), (-4,3), (8,0) та (4,3), (4,-3), (-8,0), а площа кожного трикутника — 36. Таким чином $A(8) = 36 + 36 = 72$.
Можна перевірити, що $A(10) = 252$, $A(100) = 34\\,632$ та $A(1000) = 3\\,529\\,008$.
Знайдіть $A(1\\,000\\,000\\,000)$.
1Фокусами еліпса є дві точки $A$ та $B$. Для кожної точки $P$ на межі еліпса $AP + PB$ є константою.
# --hints--
`ellipsesInsideTriangles()` має повернути `3776957309612154000`.
```js
assert.strictEqual(ellipsesInsideTriangles(), 3776957309612154000);
```
# --seed--
## --seed-contents--
```js
function ellipsesInsideTriangles() {
return true;
}
ellipsesInsideTriangles();
```
# --solutions--
```js
// solution required
```