---
id: 5900f5431000cf542c510056
title: 'Задача 471: Трикутник вписаний в еліпс'
challengeType: 5
forumTopicId: 302148
dashedName: problem-471-triangle-inscribed-in-ellipse
---
# --description--
Трикутник $ΔABC$ вписаний в еліпс з рівнянням $\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$, $0 < 2b < a$, $a$ та $b$ — цілі числа.
Нехай $r(a, b)$ — радіус вписаного в трикутник $ΔABC$ кола, де $(2b, 0)$ є центром вписаного кола, а $A$ має такі координати: $\left(\frac{a}{2}, \frac{\sqrt{3}}{2}b\right)$.
Наприклад, $r(3, 1) = \frac{1}{2}, r(6, 2) = 1, r(12, 3) = 2$.
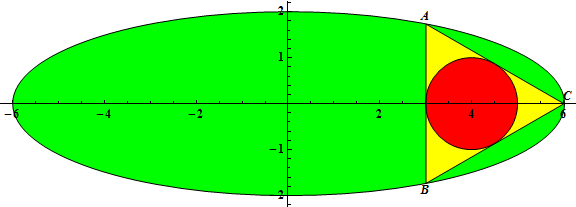
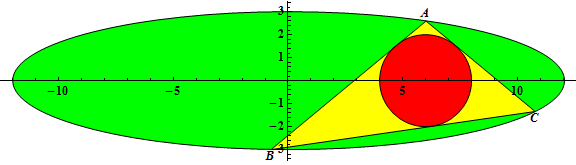 Нехай $G(n) = \sum_{a = 3}^n \sum_{b = 1}^{\left\lfloor\frac{a - 1}{2} \right\rfloor} r(a, b)$
Дано, що $G(10) = 20.59722222$, $G(100) = 19223.60980$ (заокруглено до 10 значущих цифр).
Знайдіть $G({10}^{11})$. Дайте відповідь у вигляді рядка в науковому позначенні, округленому до 10 значущих цифр. Використовуйте малу літеру `e` для відокремлення мантиси та показника степеня.
Для $G(10)$ відповідь була б такою: `2.059722222e1`
# --hints--
`triangleInscribedInEllipse()` має повернути рядок.
```js
assert(typeof triangleInscribedInEllipse() === 'string');
```
`triangleInscribedInEllipse()` має повернути рядок `1.895093981e31`.
```js
assert.strictEqual(triangleInscribedInEllipse(), '1.895093981e31');
```
# --seed--
## --seed-contents--
```js
function triangleInscribedInEllipse() {
return true;
}
triangleInscribedInEllipse();
```
# --solutions--
```js
// solution required
```
Нехай $G(n) = \sum_{a = 3}^n \sum_{b = 1}^{\left\lfloor\frac{a - 1}{2} \right\rfloor} r(a, b)$
Дано, що $G(10) = 20.59722222$, $G(100) = 19223.60980$ (заокруглено до 10 значущих цифр).
Знайдіть $G({10}^{11})$. Дайте відповідь у вигляді рядка в науковому позначенні, округленому до 10 значущих цифр. Використовуйте малу літеру `e` для відокремлення мантиси та показника степеня.
Для $G(10)$ відповідь була б такою: `2.059722222e1`
# --hints--
`triangleInscribedInEllipse()` має повернути рядок.
```js
assert(typeof triangleInscribedInEllipse() === 'string');
```
`triangleInscribedInEllipse()` має повернути рядок `1.895093981e31`.
```js
assert.strictEqual(triangleInscribedInEllipse(), '1.895093981e31');
```
# --seed--
## --seed-contents--
```js
function triangleInscribedInEllipse() {
return true;
}
triangleInscribedInEllipse();
```
# --solutions--
```js
// solution required
```

 Нехай $G(n) = \sum_{a = 3}^n \sum_{b = 1}^{\left\lfloor\frac{a - 1}{2} \right\rfloor} r(a, b)$
Дано, що $G(10) = 20.59722222$, $G(100) = 19223.60980$ (заокруглено до 10 значущих цифр).
Знайдіть $G({10}^{11})$. Дайте відповідь у вигляді рядка в науковому позначенні, округленому до 10 значущих цифр. Використовуйте малу літеру `e` для відокремлення мантиси та показника степеня.
Для $G(10)$ відповідь була б такою: `2.059722222e1`
# --hints--
`triangleInscribedInEllipse()` має повернути рядок.
```js
assert(typeof triangleInscribedInEllipse() === 'string');
```
`triangleInscribedInEllipse()` має повернути рядок `1.895093981e31`.
```js
assert.strictEqual(triangleInscribedInEllipse(), '1.895093981e31');
```
# --seed--
## --seed-contents--
```js
function triangleInscribedInEllipse() {
return true;
}
triangleInscribedInEllipse();
```
# --solutions--
```js
// solution required
```
Нехай $G(n) = \sum_{a = 3}^n \sum_{b = 1}^{\left\lfloor\frac{a - 1}{2} \right\rfloor} r(a, b)$
Дано, що $G(10) = 20.59722222$, $G(100) = 19223.60980$ (заокруглено до 10 значущих цифр).
Знайдіть $G({10}^{11})$. Дайте відповідь у вигляді рядка в науковому позначенні, округленому до 10 значущих цифр. Використовуйте малу літеру `e` для відокремлення мантиси та показника степеня.
Для $G(10)$ відповідь була б такою: `2.059722222e1`
# --hints--
`triangleInscribedInEllipse()` має повернути рядок.
```js
assert(typeof triangleInscribedInEllipse() === 'string');
```
`triangleInscribedInEllipse()` має повернути рядок `1.895093981e31`.
```js
assert.strictEqual(triangleInscribedInEllipse(), '1.895093981e31');
```
# --seed--
## --seed-contents--
```js
function triangleInscribedInEllipse() {
return true;
}
triangleInscribedInEllipse();
```
# --solutions--
```js
// solution required
```