---
title: Complex Number Plane
---
## Complex Numbers
The complex number plane expresses a complex number in graphical form. The complex number is an extension of the real number
line that adds an imaginary axis. This creates a two dimensional space with real and imaginary coordinates.
Complex numbers take the form (a + bi) with the real part being "a" expressed on the x-axis and "b" expressed on the y-axis. See the
graph below.
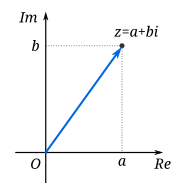 A complex number that is on the x-axis is called purely real; while a complex number that is on the y-axis only is
called purely imaginary. The x-axis or real number line includes all real numbers. Therefore, the set of all real numbers is actually
a subset of the complex numbers. All real numbers, then are complex numbers who imaginary component is zero.
## Complex Polar Coordinates
In polar form the cooordinates are the radius to the point in the complex plane and the angle from the x-axis.
The radius[r] is found from the pythagorean formula applied to the real and imaginary componenets.
r = sqrt(a^2 + b^2)
The angle for the polar coordinate is found from taking the inverse tangent of the real and imaginary coordinates.
@ = arctan(b/a) where x > 0
@ = arctan(b/a) + pi where x < 0
@ is undefined when x = 0
A complex number that is on the x-axis is called purely real; while a complex number that is on the y-axis only is
called purely imaginary. The x-axis or real number line includes all real numbers. Therefore, the set of all real numbers is actually
a subset of the complex numbers. All real numbers, then are complex numbers who imaginary component is zero.
## Complex Polar Coordinates
In polar form the cooordinates are the radius to the point in the complex plane and the angle from the x-axis.
The radius[r] is found from the pythagorean formula applied to the real and imaginary componenets.
r = sqrt(a^2 + b^2)
The angle for the polar coordinate is found from taking the inverse tangent of the real and imaginary coordinates.
@ = arctan(b/a) where x > 0
@ = arctan(b/a) + pi where x < 0
@ is undefined when x = 0
 #### More Information
-[Wikipedia:Complex number](https://en.wikipedia.org/wiki/Complex_number)
-[Wolfram](http://mathworld.wolfram.com/ComplexNumber.html)
#### More Information
-[Wikipedia:Complex number](https://en.wikipedia.org/wiki/Complex_number)
-[Wolfram](http://mathworld.wolfram.com/ComplexNumber.html)
 A complex number that is on the x-axis is called purely real; while a complex number that is on the y-axis only is
called purely imaginary. The x-axis or real number line includes all real numbers. Therefore, the set of all real numbers is actually
a subset of the complex numbers. All real numbers, then are complex numbers who imaginary component is zero.
## Complex Polar Coordinates
In polar form the cooordinates are the radius to the point in the complex plane and the angle from the x-axis.
The radius[r] is found from the pythagorean formula applied to the real and imaginary componenets.
r = sqrt(a^2 + b^2)
The angle for the polar coordinate is found from taking the inverse tangent of the real and imaginary coordinates.
@ = arctan(b/a) where x > 0
@ = arctan(b/a) + pi where x < 0
@ is undefined when x = 0
A complex number that is on the x-axis is called purely real; while a complex number that is on the y-axis only is
called purely imaginary. The x-axis or real number line includes all real numbers. Therefore, the set of all real numbers is actually
a subset of the complex numbers. All real numbers, then are complex numbers who imaginary component is zero.
## Complex Polar Coordinates
In polar form the cooordinates are the radius to the point in the complex plane and the angle from the x-axis.
The radius[r] is found from the pythagorean formula applied to the real and imaginary componenets.
r = sqrt(a^2 + b^2)
The angle for the polar coordinate is found from taking the inverse tangent of the real and imaginary coordinates.
@ = arctan(b/a) where x > 0
@ = arctan(b/a) + pi where x < 0
@ is undefined when x = 0
 #### More Information
-[Wikipedia:Complex number](https://en.wikipedia.org/wiki/Complex_number)
-[Wolfram](http://mathworld.wolfram.com/ComplexNumber.html)
#### More Information
-[Wikipedia:Complex number](https://en.wikipedia.org/wiki/Complex_number)
-[Wolfram](http://mathworld.wolfram.com/ComplexNumber.html)