---
title: Derivative
---
## Derivative
**Definition** : The derivative of function f(x) with respect to x, represented by f'(x) is defined as:

where h is a infinitely small change in the value of input, represented by the limit function (h is approaching to zero)
In the above formula, we notice that derivative is just the slope of a tangent of a graph of x at any input value.
**Important property of function and it's derivative:**
A function f(x) is differentiable at x = a, if and only if, the function is continuous at f(x=a).
Conversely, if a derivative of a function exists at a point a, then the function must be continous at f(x=a).
## Properties of Derivatives
1. **Linearity**
Suppose f(x) and g(x) are differentiable functions and a and b are real numbers. Then the function
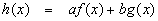
is differentiable as
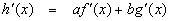
2. **Product Rule**
For a given function h(x) = f(x) * g(x), we can apply the product rule to find the derivative of function h(x) as
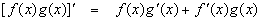
Please see link in More information (Properties of Derivative) for proof of this property
3. **Quotient Rule**
The quotient rule gives the derivative of one function divided by another. Let h(x) = f(x) / g(x) (where g(x) cannot be zero) then the derivative of h(x) can be found using the following:
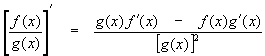
Please see link in More information (Properties of Derivative) for proof of this property
4. **Chain Rule**
The chain rule is used in the case of a function of a function, also known as a composite function or as a composition of functions. Input composite function representation:
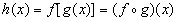
Then the output derivative can be found using the following rule:
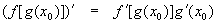
Please see link in More information (Properties of Derivative) for proof of this property
#### More Information:
http://tutorial.math.lamar.edu/Classes/CalcI/DerivativeIntro.aspx
http://tutorial.math.lamar.edu/Classes/CalcI/DefnOfDerivative.aspx
Properies of derivatives (proofs included) : http://www.hyper-ad.com/tutoring/math/calculus/Properties_of_Derivatives.html
**Note** : Images taken from http://www.hyper-ad.com/ and http://tutorial.math.lamar.edu/