2.4 KiB
title, localeTitle
| title | localeTitle |
|---|---|
| Piecewise Functions Graphs | Графы составных функций |
Графы составных функций
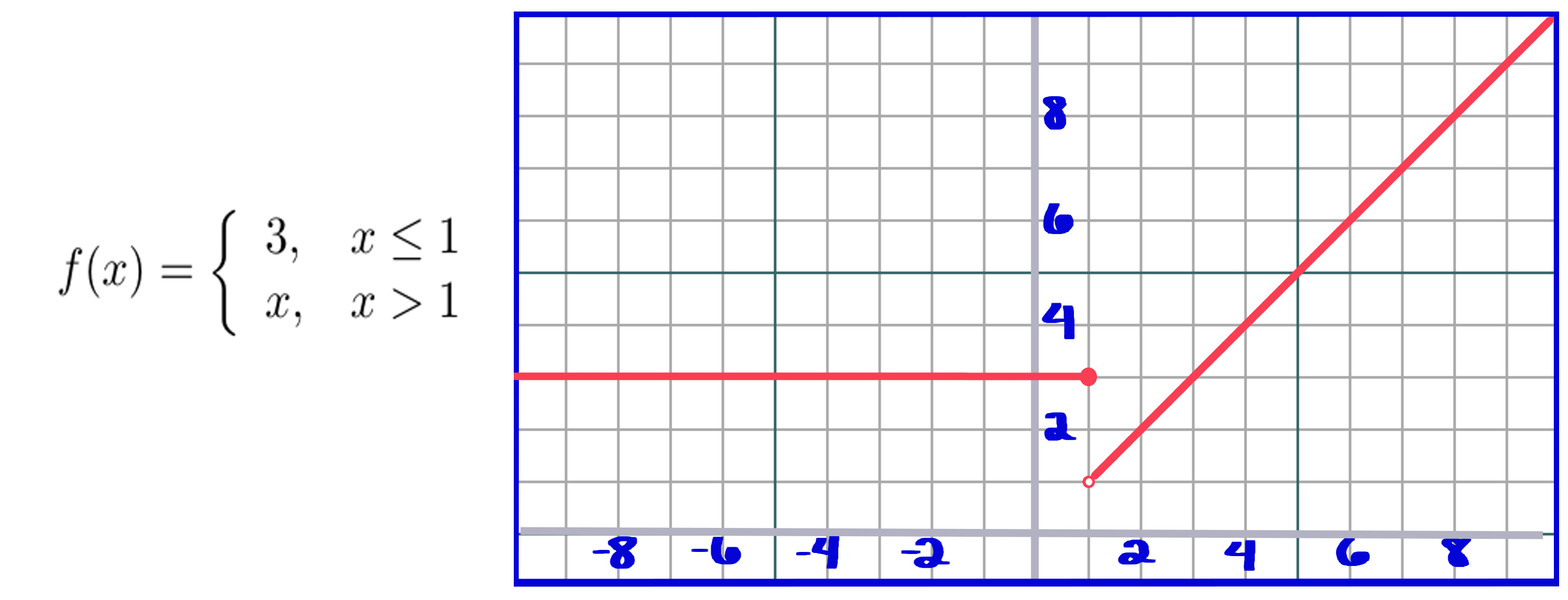
Кусочные функции определяются по-разному для разных интервалов x . Чтобы найти y , вы используете x для поиска того, на каком интервал он находится. Давайте рассмотрим простую кусочную функцию и ее график.
Вы можете видеть, что когда x меньше или равно 1, y равно 3, а когда x больше 1, y равно x. Это почти как кусочные функции, созданные путем объединения различных функций в одно.
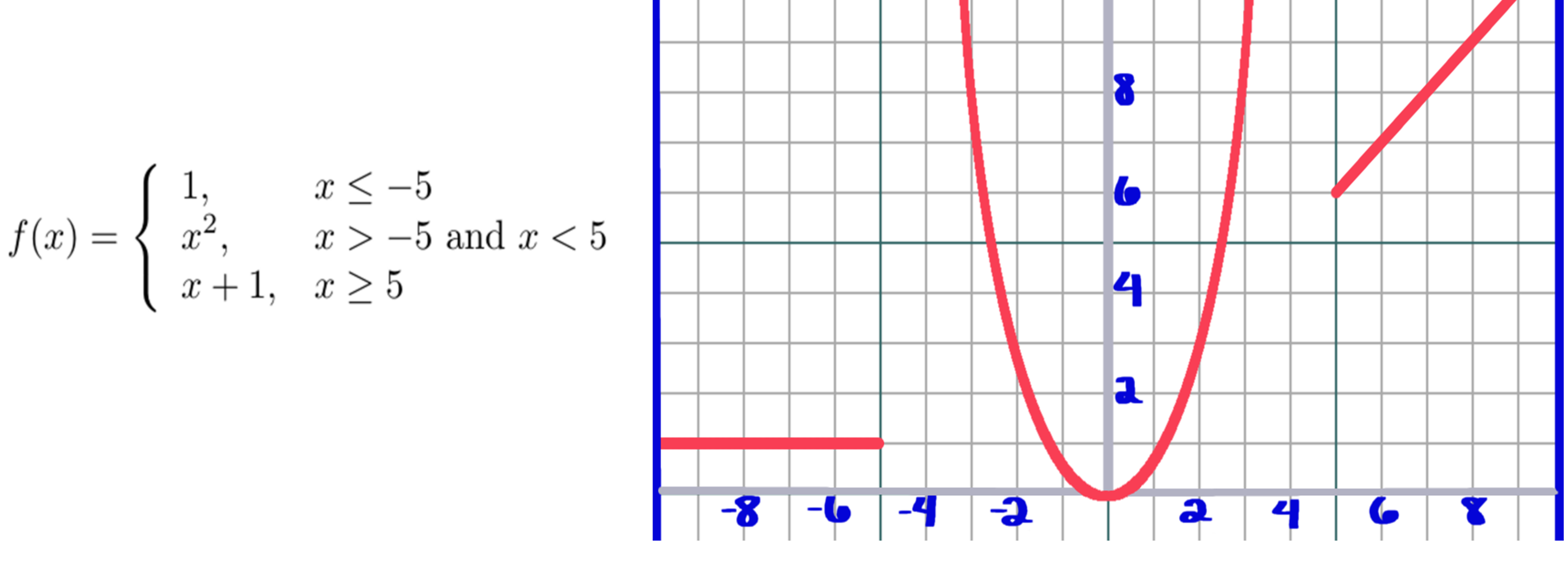
На приведенном выше графике вы можете увидеть, что квадрат x может быть автономной функцией, которая будет определена для всех действительных чисел. Вместо этого мы определили нашу кусочную функцию, поэтому только значения x , которые больше, чем -5 и меньше 5, вводятся в квадрат x . Обратите внимание, что этот граф имеет две «граничные линии» при x = -5 и x = 5 , а первый график имеет одну «граничную линию» при x = 1 .
Непрерывные / Непрерывные кусочные функции
Как вы можете определить, непрерывна ли какая-либо конкретная кусочная функция? Давайте рассмотрим пару примеров.