1.9 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f4971000cf542c50ffaa | Problema 299: Três triângulos similares | 5 | 301951 | problem-299-three-similar-triangles |
--description--
Quatro pontos com coordenadas em números inteiros são selecionadas:
A(a, 0), B(b, 0), C(0, c) e D(0, d), com 0 < a < b and 0 < c < d.
O ponto P, também com coordenadas em número inteiros, é escolhido na linha AC de modo que os três triângulos, ABP, CDP e BDP, são todos similares.
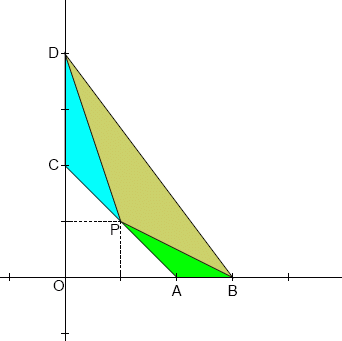
É fácil provar que os três triângulos podem ser similares apenas se a = c.
Então, dado que a = c, estamos procurando por trios (a, b, d), de modo que pelo menos um ponto P (com coordenadas em números inteiros) existe em AC, tornando todos os três triângulos ABP, CDP e BDP similares.
Por exemplo, se (a, b, d) = (2, 3, 4), pode ser facilmente verificado que o ponto P(1, 1) satisfaz a condição acima. Observe que os trios (2,3,4) e (2,4,3) são considerados distintos, embora o ponto P(1, 1) seja comum para ambos.
Se b + d < 100, existem 92 trios distintos (a, b, d) de modo que o ponto P exista.
Se b + d < 100.000, existem 320471 trios distintos (a, b, d) de modo que o ponto P exista.
Se b + d < 100.000.000, quantos trios distintos (a, b, d) existem de modo que o ponto P exista?
--hints--
threeSimilarTriangles() deve retornar 549936643.
assert.strictEqual(threeSimilarTriangles(), 549936643);
--seed--
--seed-contents--
function threeSimilarTriangles() {
return true;
}
threeSimilarTriangles();
--solutions--
// solution required