1.4 KiB
1.4 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f5001000cf542c510012 | Problema 404: Elipses cruzadas | 5 | 302072 | problem-404-crisscross-ellipses |
--description--
E_a é uma elipse com a equação na forma x^2 + 4y^2 = 4a^2.
E_a' é a imagem rodada de E_a por θ graus no sentido anti-horário ao redor da origem O(0, 0) para 0° < θ < 90°.
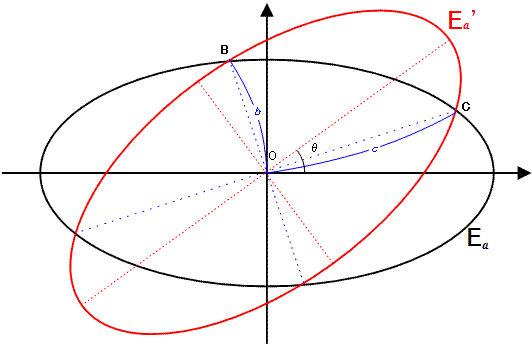
b é a distância da origem dos dois pontos de interseção mais próximos da origem e c é a distância dos outros dois pontos de interseção.
Chamaremos um trio ordenado (a, b, c) de trio elipsoidal canônico se a, b e c forem números inteiros positivos.
Por exemplo, (209, 247, 286) é um trio elipsoidal canônico.
Considere C(N) como o número de trios elipsoidais canônicos (a, b, c) distintos para a ≤ N.
Pode-se verificar que C({10}^3) = 7, C({10}^4) = 106 e C({10}^6) = 11.845.
Encontre C({10}^{17}).
--hints--
crisscrossEllipses() deve retornar 1199215615081353.
assert.strictEqual(crisscrossEllipses(), 1199215615081353);
--seed--
--seed-contents--
function crisscrossEllipses() {
return true;
}
crisscrossEllipses();
--solutions--
// solution required