freeCodeCamp/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-385-ellipses-inside-triangles.md

id, title, challengeType, forumTopicId, dashedName

id	title	challengeType	forumTopicId	dashedName
5900f4ee1000cf542c510000	Problema 385: Elipses dentro de triângulos	5	302049	problem-385-ellipses-inside-triangles

--description--

Para qualquer triângulo T no plano, pode-se mostrar que há uma elipse única com a maior área completamente dentro de T.

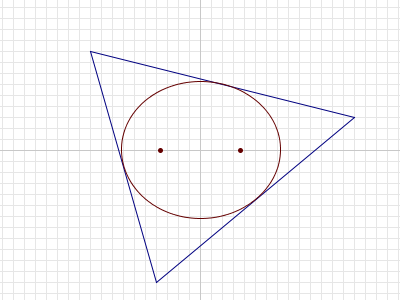
Para um n dado, considere os triângulos T, tal que:

• os vértices de T têm coordenadas em números inteiros, com valor absoluto ≤ n, e
• os focos¹ da elipse de maior área dentro de T são (\sqrt{13}, 0) e (-\sqrt{13}, 0).

Considere A(n) como a soma das áreas de todos esses triângulos.

Por exemplo, se n = 8, existem dois triângulos desse tipo. Seus vértices são (-4,-3), (-4,3), (8,0) e (4,3), (4,-3), (-8,0). A área de cada triângulo é 36. Portanto, A(8) = 36 + 36 = 72.

Pode-se verificar que A(10) = 252, A(100) = 34.632 e A(1000) = 3.529.008.

Encontre A(1.000.000.000).

¹Os focos de uma elipse são dois pontos A e B, tal que, para qualquer ponto P no limite da elipse, AP + PB é constante.

--hints--

ellipsesInsideTriangles() deve retornar 3776957309612154000.

assert.strictEqual(ellipsesInsideTriangles(), 3776957309612154000);

--seed--

--seed-contents--

function ellipsesInsideTriangles() {

  return true;
}

ellipsesInsideTriangles();

--solutions--

// solution required