freeCodeCamp/guide/arabic/mathematics/derivative/index.md

title, localeTitle

title	localeTitle
Derivative	المشتق

المشتق

التعريف : يُعرَّف مشتق الدالة f (x) بالنسبة إلى x ، الممثلة بـ f '(x) على النحو التالي:

حيث h هو تغير طفيف بشكل لا نهائي في قيمة المدخلات ، ممثلة بوظيفة الحد (يقترب من الصفر إلى الصفر)

في الصيغة المذكورة أعلاه ، نلاحظ أن المشتق هو مجرد منحدر ظل من رسم بياني × عند أي قيمة إدخال.

خاصية مهمة للوظيفة ومشتقاتها:
تكون الدالة f (x) قابلة للتفاضل عند x = a ، إذا و ، فقط إذا كانت الوظيفة مستمرة عند f (x = a).
وعلى العكس من ذلك ، إذا كانت مشتقة دالة موجودة عند النقطة a ، فيجب أن تكون الدالة متواصلة عند f (x = a).

خصائص المشتقات

1. الخطي
   لنفترض أن f (x) و g (x) هما دالتان مختلفتان ، وأن a و b هما أرقاما حقيقية. ثم الوظيفة
   
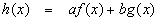
   هو الاختلاف
   

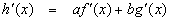
2. سيادة المنتج
   بالنسبة لوظيفة معينة h (x) = f (x) * g (x) ، يمكننا تطبيق قاعدة المنتج للبحث عن مشتق الدالة h (x) مثل
   
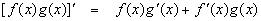
   يرجى الاطلاع على الرابط في مزيد من المعلومات (خصائص مشتق) لإثبات هذه الخاصية

3. قاعدة الحسم
   تعطي قاعدة الحاصل المشتق لوظيفة واحدة مقسومة على أخرى. دع h (x) = f (x) / g (x) (حيث g (x) لا يمكن أن يكون صفراً) ثم يمكن العثور على مشتق h (x) باستخدام ما يلي:
   
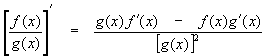
   يرجى الاطلاع على الرابط في مزيد من المعلومات (خصائص مشتق) لإثبات هذه الخاصية

4. قاعدة سلسلة
   تُستخدم قاعدة السلسلة في حالة دالة دالة ، تُعرف أيضًا باسم دالة مركبة أو كتكوين للوظائف. تمثيل وظيفة التمثيل المركب:
   
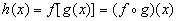
   ثم يمكن العثور على مشتق الإخراج باستخدام القاعدة التالية:
   
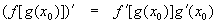
   يرجى الاطلاع على الرابط في مزيد من المعلومات (خصائص مشتق) لإثبات هذه الخاصية

معلومات اكثر:

http://tutorial.math.lamar.edu/Classes/CalcI/DerivativeIntro.aspx http://tutorial.math.lamar.edu/Classes/CalcI/DefnOfDerivative.aspx خصائص المشتقات (بما في ذلك البراهين): http://www.hyper-ad.com/tutoring/math/calculus/Properties of Derivatives.html

ملاحظة : الصور مأخوذة من http://www.hyper-ad.com/ و http://tutorial.math.lamar.edu/