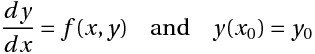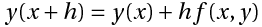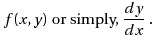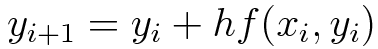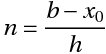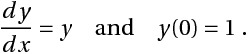2.3 KiB
2.3 KiB
title, localeTitle
| title | localeTitle |
|---|---|
| Euler's Method | 欧拉方法 |
欧拉方法
Euler方法是用于求解具有给定初始值的常微分方程（ODE）的一阶数值过程。
一般初值问题
方法
欧拉的方法使用简单的公式，
在点x处构造切线并获得y(x+h) ，其斜率为，
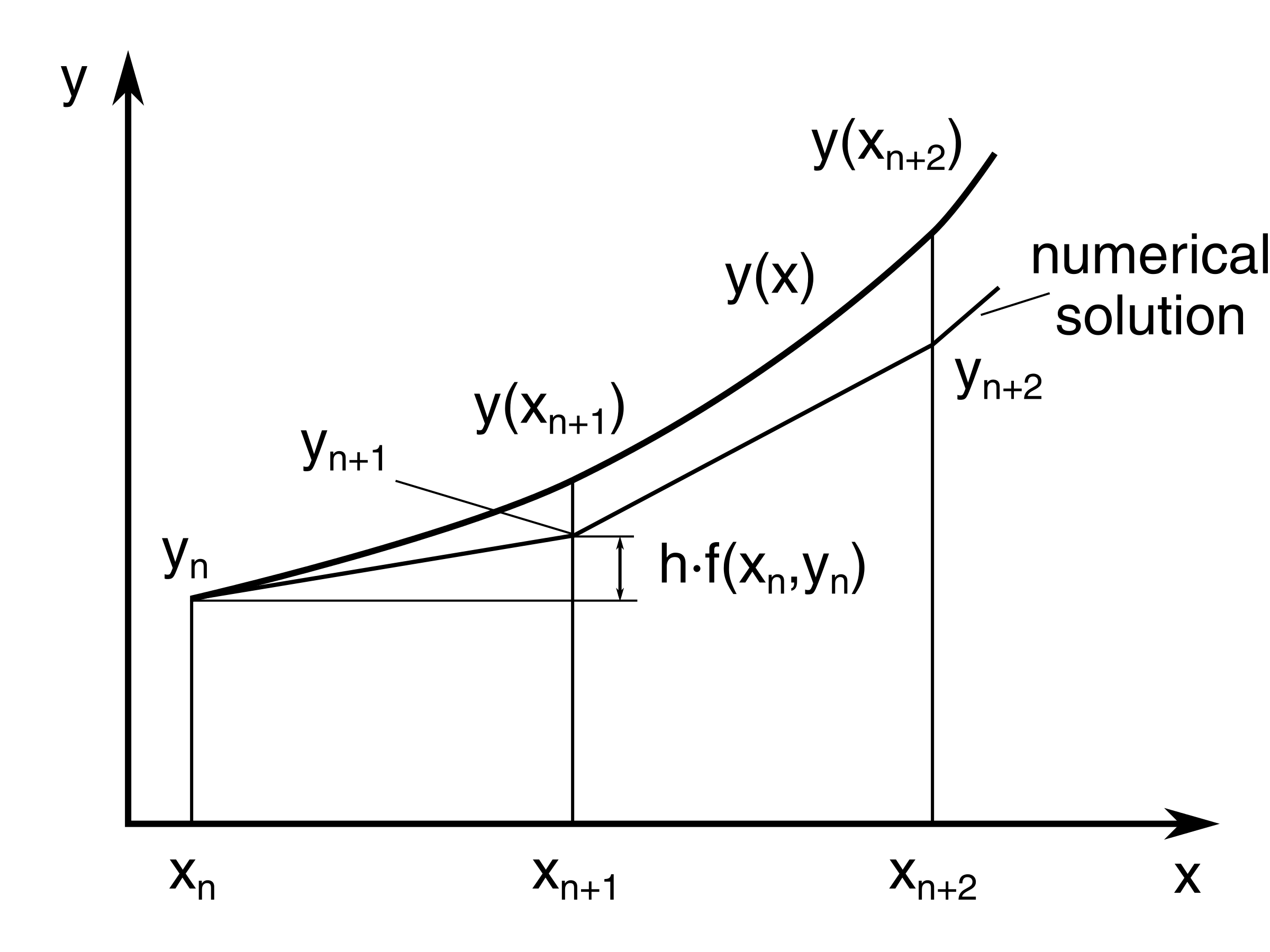
在欧拉方法中，您可以通过每个区间中的切线（即一系列短线段）以h步长逼近解的曲线。
通常 ，如果使用小步长，则近似的精度会增加。
通式
任意点b功能值，由y(b)
哪里，
- n =步数
- h =间隔宽度（每一步的大小）
伪代码
例
找到y(1) ，给定
通过分析求解，解是_y = e x_和y(1) = 2.71828 。 （注意：此分析解决方案仅用于比较准确性。）
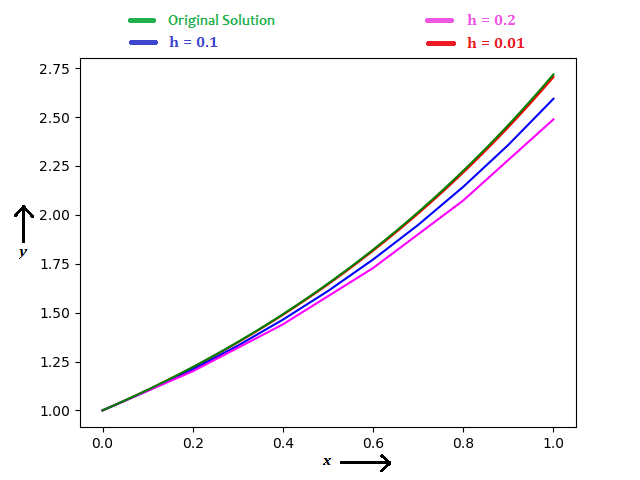
使用欧拉法，考虑h = 0.2 ， 0.1 ， 0.01 ，可以看到以下的图中的结果。
当h = 0.2 ， y(1) = 2.48832 （误差= 8.46％）
当h = 0.1 ， y(1) = 2.59374 （误差= 4.58％）
当h = 0.01 ， y(1) = 2.70481 （误差= 0.50％）
您可以注意到，当步数很小时，准确度如何提高。