freeCodeCamp/guide/spanish/algorithms/greatest-common-divisor-euclidean/index.md

---
title: Greatest Common Divisor Euclidean
localeTitle: El mayor divisor común euclidiano
---
## El mayor divisor común euclidiano

Para este tema, debe conocer primero el Divisor común más grande (GCD) y la operación MOD.

#### El divisor común más grande (GCD)

El GCD de dos o más enteros es el entero más grande que divide cada uno de los enteros de tal manera que su resto es cero.

Ejemplo-  
GCD de 20, 30 = 10 _(10 es el número más grande que divide 20 y 30 con el resto como 0)_  
GCD de 42, 120, 285 = 3 _(3 es el número más grande que divide a 42, 120 y 285 con el resto como 0)_

#### Operación "mod"

La operación de modificación le da el resto cuando se dividen dos enteros positivos. Lo escribimos como sigue:  
`A mod B = R`

Esto significa que dividir A por B le da el resto R, esto es diferente de la operación de división que le da el cociente.

Ejemplo-  
7 mod 2 = 1 _(Dividir 7 por 2 da el resto 1)_  
42 mod 7 = 0 _(Dividir 42 por 7 da el resto 0)_

Con los dos conceptos anteriores entendidos, comprenderá fácilmente el Algoritmo Euclidiano.

### Algoritmo euclidiano para el divisor común más grande (GCD)

El algoritmo euclidiano encuentra el GCD de 2 números.

Comprenderás mejor este algoritmo viéndolo en acción. Suponiendo que desea calcular el GCD de 1220 y 516, apliquemos el algoritmo euclídeo -

Suponiendo que desea calcular el GCD de 1220 y 516, apliquemos el algoritmo euclídeo - ![Ejemplo Euclidiano](https://cdn-media-1.freecodecamp.org/imgr/aa8oGgP.png)

Pseudo Código del algoritmo  
Paso 1: **Sean `a, b` los dos números**  
Paso 2: **`a mod b = R`**  
Paso 3: **Deje que `a = b` y `b = R`**  
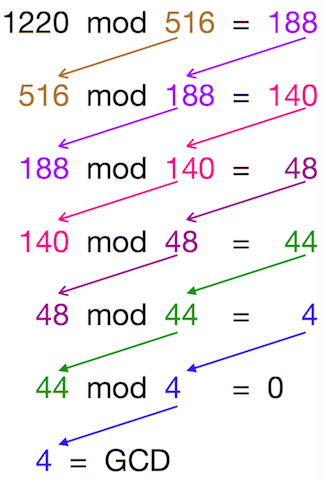
Paso 4: **repita los pasos 2 y 3 hasta que `a mod b` sea ​​mayor que 0**  
Paso 5: **GCD = b**  
Paso 6: Finalizar

Código Javascript para realizar GCD-

```javascript
function gcd(a, b) { 
  var R; 
  while ((a % b) > 0)  { 
    R = a % b; 
    a = b; 
    b = R; 
  } 
  return b; 
 } 
```

Código Javascript para realizar GCD usando Recursion-

```javascript
function gcd(a, b) { 
  if (b == 0) 
    return a; 
  else 
    return gcd(b, (a % b)); 
 } 
```

También puede usar el algoritmo euclídeo para encontrar GCD de más de dos números. Como GCD es asociativo, la siguiente operación es válida: `GCD(a,b,c) == GCD(GCD(a,b), c)`

Calcule el GCD de los dos primeros números, luego encuentre el GCD del resultado y el siguiente número. Ejemplo: `GCD(203,91,77) == GCD(GCD(203,91),77) == GCD(7, 77) == 7`

Puedes encontrar GCD de `n` números de la misma manera.