21 lines
1.2 KiB
Markdown
21 lines
1.2 KiB
Markdown
|
|
---
|
|||
|
|
title: Piecewise Functions Graphs
|
|||
|
|
localeTitle: 分段函数图
|
|||
|
|
---
|
|||
|
|
## 分段函数图
|
|||
|
|
|
|||
|
|
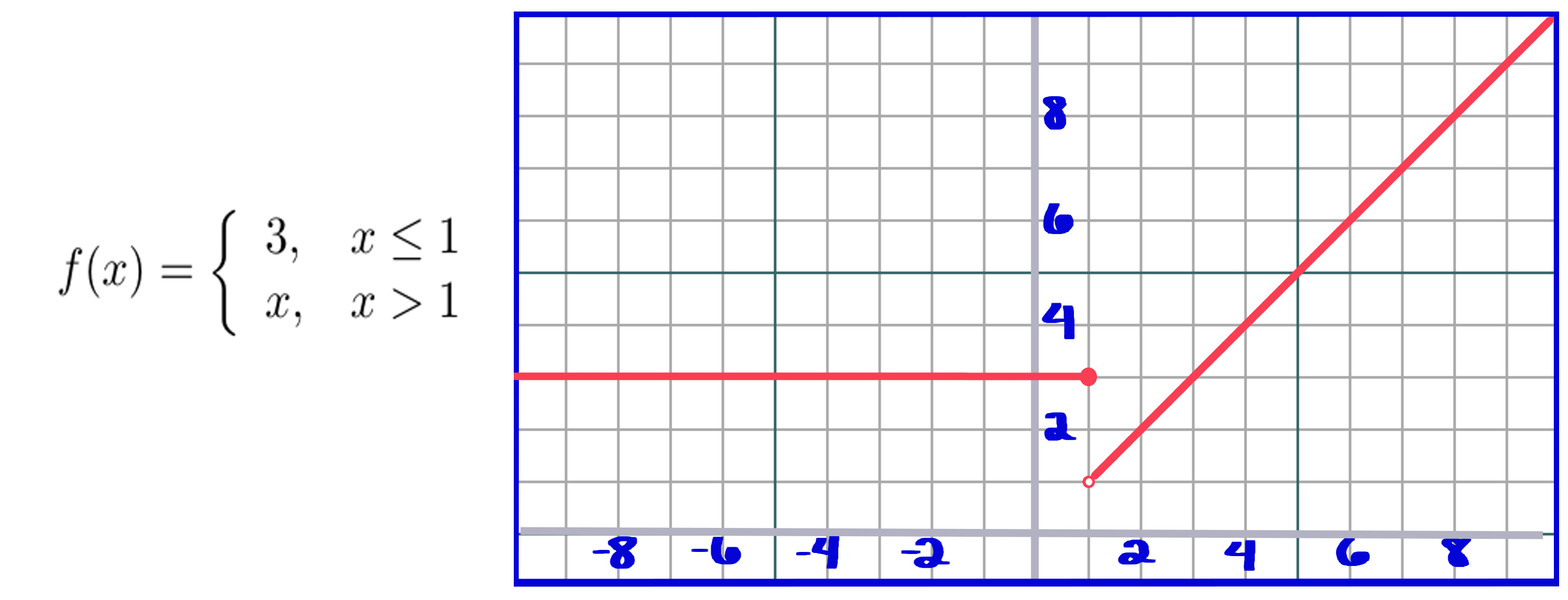
对于`x`不同间隔,分段函数的定义不同。为了找到`y` ,你使用`x`来查找它所处的间隔。让我们看一个简单的分段函数及其图形。
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
您可以看到,当`x`小于或等于1时, `y`等于3,当`x`大于1时, `y`等于x。它几乎就像通过将不同的功能组合成一个来创建分段功能。
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
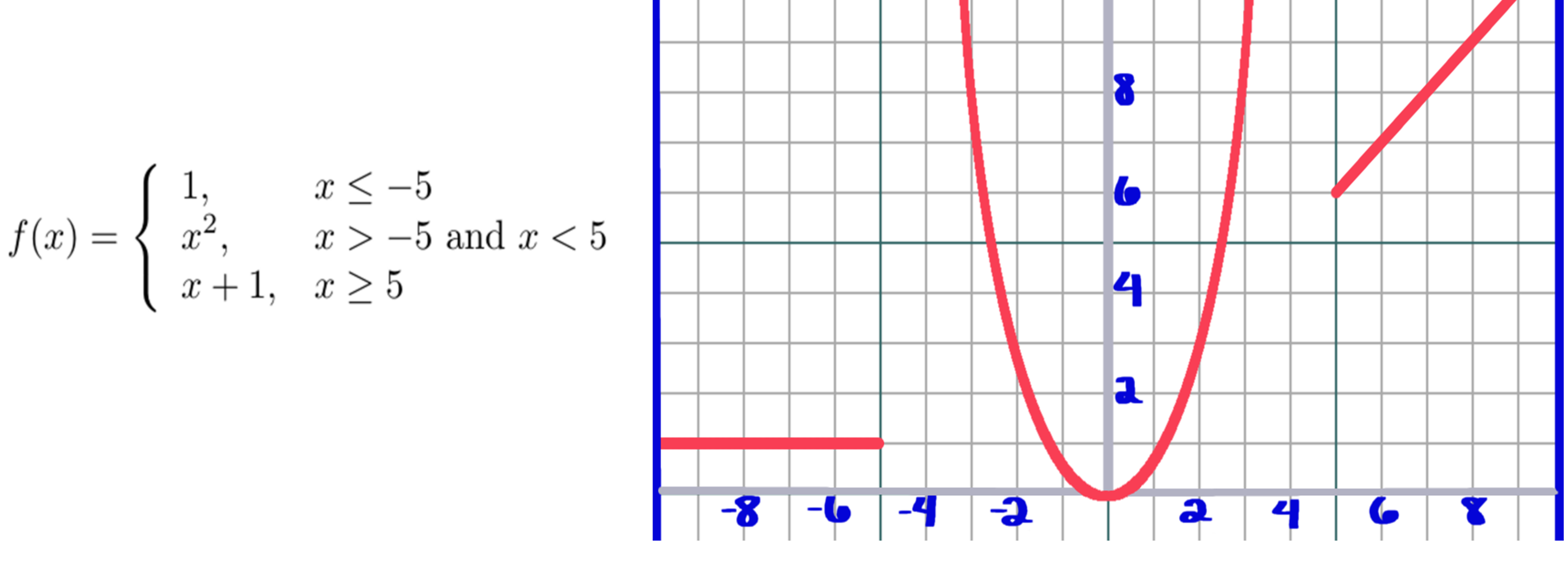
在上图中,您可以看到`x`平方可以是一个独立的函数,它将为所有实数定义。相反,我们已经定义了分段函数,因此只有大于-5且小于5的`x`值才输入到`x`平方。请注意,此图形在`x = -5`和`x = 5`似乎有两条“边界线”,第一条图形在`x = 1`处有一条“边界线”。
|
|||
|
|
|
|||
|
|
### 连续/非连续分段函数
|
|||
|
|
|
|||
|
|
如何判断特定的分段函数是否连续?我们来看几个例子。
|
|||
|
|
|
|||
|
|

|