141 lines
4.8 KiB
Markdown
141 lines
4.8 KiB
Markdown
|
|
---
|
|||
|
|
title: Freecodecamp Algorithm Merge Sort Guide
|
|||
|
|
localeTitle: Freecodecamp算法合并排序指南
|
|||
|
|
---
|
|||
|
|
大多数现代语言都有内置的sort()函数,可以自动对输入数组或列表进行排序。你有没有想过排序功能如何在内部实际工作?了解常见的排序算法及其实现是编码访谈中最重要的部分。在本系列文章中,我们将介绍几种重要的排序算法。它们是如何实现的,时间和空间的复杂性等。我们的第一篇文章是Merge Sort。
|
|||
|
|
|
|||
|
|
要了解Merge Sort,有关[递归](http://programmers.stackexchange.com/questions/25052/in-plain-english-what-is-recursion)的基本知识是先决条件。 Merge Sort基于Divide and Conquer原则。对N个整数数组进行排序的整个过程可归纳为三个步骤 -
|
|||
|
|
|
|||
|
|
* 将阵列分成两半。
|
|||
|
|
* 使用相同的重复算法对左半部分和右半部分进行排序。
|
|||
|
|
* 合并分类的一半。
|
|||
|
|
|
|||
|
|
使用Merge排序的最大优点是[时间复杂度](https://www.youtube.com/watch?v=V42FBiohc6c&list=PL2_aWCzGMAwI9HK8YPVBjElbLbI3ufctn)仅为n \* log(n)以对整个Array进行排序。它比冒泡排序或插入排序的n ^ 2运行时间要好很多。
|
|||
|
|
|
|||
|
|
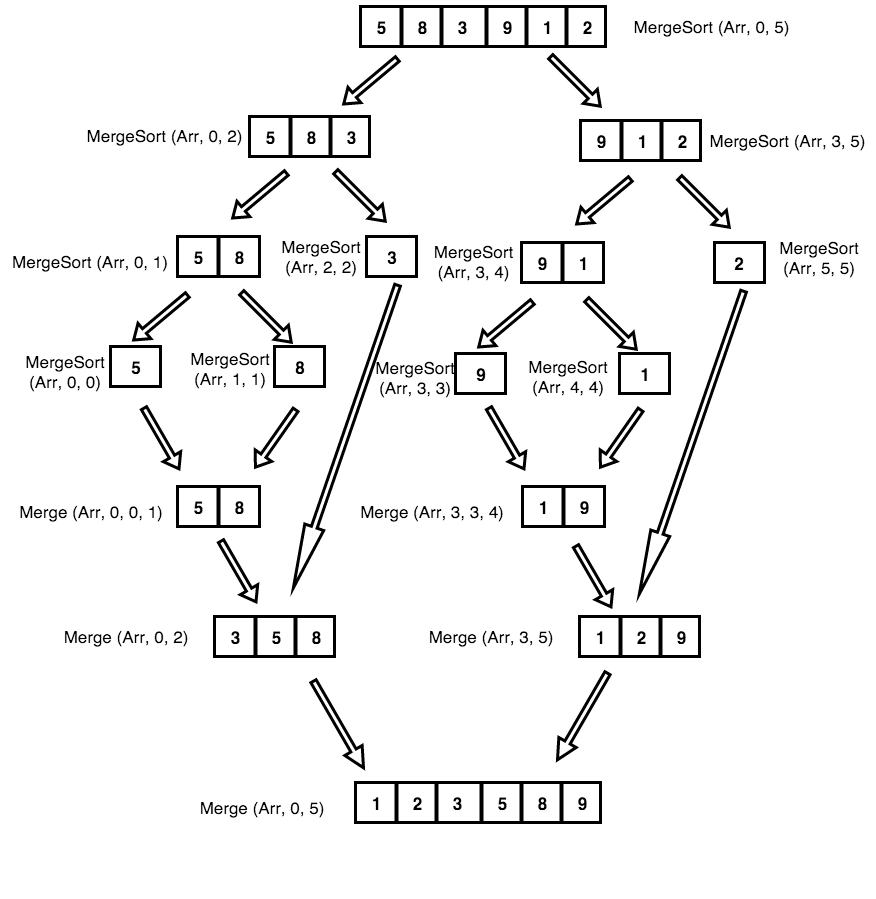
在编写代码之前,让我们在图表的帮助下理解合并排序的工作原理。
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
* 最初我们有一个包含6个未排序整数的数组Arr(5,8,3,9,1,2)
|
|||
|
|
* 我们将阵列分成两半Arr1 =(5,8,3)和Arr2 =(9,1,2)。
|
|||
|
|
* 再次,我们将它们分成两半:Arr3 =(5,8)和Arr4 =(3)和Arr5 =(9,1)和Arr6 =(2)
|
|||
|
|
* 再次,我们将它们分成两半:Arr7 =(5),Arr8 =(8),Arr9 =(9),Arr10 =(1)和Arr6 =(2)
|
|||
|
|
* 我们现在将比较这些子数组中的元素以合并它们。
|
|||
|
|
|
|||
|
|
## 履行
|
|||
|
|
|
|||
|
|
### C ++实现
|
|||
|
|
```
|
|||
|
|
void merge(int array[], int left, int mid, int right)
|
|||
|
|
{
|
|||
|
|
int i, j, k;
|
|||
|
|
|
|||
|
|
// Size of left sublist
|
|||
|
|
int size_left = mid - left + 1;
|
|||
|
|
|
|||
|
|
// Size of right sublist
|
|||
|
|
int size_right = right - mid;
|
|||
|
|
|
|||
|
|
/* create temp arrays */
|
|||
|
|
int Left[size_left], Right[size_right];
|
|||
|
|
|
|||
|
|
/* Copy data to temp arrays L[] and R[] */
|
|||
|
|
for(i = 0; i < size_left; i++)
|
|||
|
|
{
|
|||
|
|
Left[i] = array[left+i];
|
|||
|
|
}
|
|||
|
|
|
|||
|
|
for(j = 0; j < size_right; j++)
|
|||
|
|
{
|
|||
|
|
Right[j] = array[mid+1+j];
|
|||
|
|
}
|
|||
|
|
|
|||
|
|
// Merge the temp arrays back into arr[left..right]
|
|||
|
|
i = 0; // Initial index of left subarray
|
|||
|
|
j = 0; // Initial index of right subarray
|
|||
|
|
k = left; // Initial index of merged subarray
|
|||
|
|
|
|||
|
|
while (i < size_left && j < size_right)
|
|||
|
|
{
|
|||
|
|
if (Left[i] <= Right[j])
|
|||
|
|
{
|
|||
|
|
array[k] = Left[i];
|
|||
|
|
i++;
|
|||
|
|
}
|
|||
|
|
else
|
|||
|
|
{
|
|||
|
|
array[k] = Right[j];
|
|||
|
|
j++;
|
|||
|
|
}
|
|||
|
|
k++;
|
|||
|
|
}
|
|||
|
|
|
|||
|
|
// Copy the remaining elements of Left[]
|
|||
|
|
while (i < size_left)
|
|||
|
|
{
|
|||
|
|
array[k] = Left[i];
|
|||
|
|
i++;
|
|||
|
|
k++;
|
|||
|
|
}
|
|||
|
|
|
|||
|
|
// Copy the rest elements of R[]
|
|||
|
|
while (j < size_right)
|
|||
|
|
{
|
|||
|
|
array[k] = Right[j];
|
|||
|
|
j++;
|
|||
|
|
k++;
|
|||
|
|
}
|
|||
|
|
}
|
|||
|
|
|
|||
|
|
void mergeSort(int array[], int left, int right)
|
|||
|
|
{
|
|||
|
|
if(left < right)
|
|||
|
|
{
|
|||
|
|
int mid = (left+right)/2;
|
|||
|
|
|
|||
|
|
// Sort first and second halves
|
|||
|
|
mergeSort(array, left, mid);
|
|||
|
|
mergeSort(array, mid+1, right);
|
|||
|
|
|
|||
|
|
// Finally merge them
|
|||
|
|
merge(array, left, mid, right);
|
|||
|
|
}
|
|||
|
|
}
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
 [运行代码](https://repl.it/CYVc/1)
|
|||
|
|
|
|||
|
|
### Javascript实现
|
|||
|
|
|
|||
|
|
我们在JavaScript中编写MergeSort:
|
|||
|
|
```
|
|||
|
|
function mergeSort (arr) {
|
|||
|
|
if (arr.length < 2) return arr;
|
|||
|
|
var mid = Math.floor(arr.length /2);
|
|||
|
|
var subLeft = mergeSort(arr.slice(0,mid));
|
|||
|
|
var subRight = mergeSort(arr.slice(mid));
|
|||
|
|
return merge(subLeft, subRight);
|
|||
|
|
}
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
首先,我们检查数组的长度。如果它是1那么我们只返回数组。这将是我们的基本情况。否则,我们将找出中间值并将数组分成两半。我们现在将对MergeSort函数的递归调用对两个部分进行排序。
|
|||
|
|
```
|
|||
|
|
function merge (a,b) {
|
|||
|
|
var result = [];
|
|||
|
|
while (a.length >0 && b.length >0)
|
|||
|
|
result.push(a[0] < b[0]? a.shift() : b.shift());
|
|||
|
|
return result.concat(a.length? a : b);
|
|||
|
|
}
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
当我们合并两个半时,我们将结果存储在辅助数组中。我们将左数组的起始元素与右数组的起始元素进行比较。哪个较小的将被推入结果数组中,我们将使用\[shift()运算符从相应的数组中删除它。如果我们最终得到左或右数组中的值,我们只需在结果的末尾连接它。这是排序结果:
|
|||
|
|
```
|
|||
|
|
var test = [5,6,7,3,1,3,15];
|
|||
|
|
console.log(mergeSort(test));
|
|||
|
|
|
|||
|
|
>> [1, 3, 3, 5, 6, 7, 15]
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
 [运行代码](https://repl.it/CYVd)
|
|||
|
|
|
|||
|
|
如果您仍然无法理解MergeSort, [视频说明](https://www.youtube.com/watch?v=TzeBrDU-JaY)将使其更加清晰。
|