2018-10-12 16:35:31 -04:00
---
title: Greatest Common Divisor Euclidean
localeTitle: Maior Divisor Comum Euclidiano
---
## Maior Divisor Comum Euclidiano
Para este tópico, você deve saber sobre o Greatest Common Divisor (GCD) e a operação MOD primeiro.
#### Maior Divisor Comum (GCD)
O GCD de dois ou mais inteiros é o maior número inteiro que divide cada um dos números inteiros, de modo que o restante seja zero.
Exemplo-
GCD de 20, 30 = 10 _ (10 é o maior número que divide 20 e 30 com o restante como 0) _
GCD de 42, 120, 285 = 3 _ (3 é o maior número que divide 42, 120 e 285 com o restante como 0) _
#### Operação "mod"
A operação mod fornece o restante quando dois inteiros positivos são divididos. Nós escrevemos como segue-
`A mod B = R`
Isto significa que dividir A por B lhe dá o resto R, isto é diferente de sua operação de divisão que lhe dá o quociente.
Exemplo-
7 mod 2 = 1 _ (dividindo 7 por 2 dá o resto 1) _
42 mod 7 = 0 _ (dividindo 42 por 7 dá o resto 0) _
Com os dois conceitos acima compreendidos, você compreenderá facilmente o Algoritmo Euclidiano.
### Algoritmo Euclidiano para o Maior Divisor Comum (GCD)
O Algoritmo Euclidiano encontra o GCD de 2 números.
Você entenderá melhor esse Algoritmo ao vê-lo em ação. Supondo que você queira calcular o GCD de 1220 e 516, vamos aplicar o Algoritmo Euclidiano -
2019-05-25 00:00:23 +03:00
Supondo que você queira calcular o GCD de 1220 e 516, vamos aplicar o Algoritmo Euclidiano - 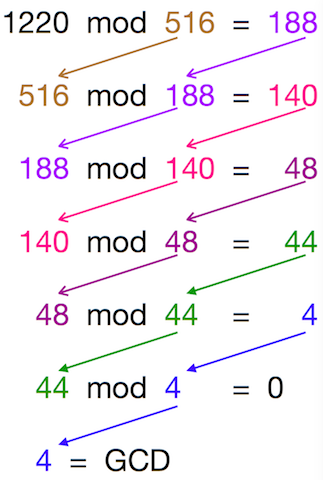
2018-10-12 16:35:31 -04:00
Pseudocódigo do Algoritmo
Etapa 1: **Seja `a, b` os dois números **
Etapa 2: * * `a mod b = R` **
Etapa 3: **deixe `a = b` e `b = R` **
Passo 4: **Repita os passos 2 e 3 até que o `a mod b` seja maior que 0 **
Etapa 5: **GCD = b **
Etapa 6: finalizar
Código JavaScript para executar o GCD-
```javascript
function gcd(a, b) {
var R;
while ((a % b) > 0) {
R = a % b;
a = b;
b = R;
}
return b;
}
```
2019-08-07 20:55:02 -03:00
Código Javascript para executar o GCD usando Recursão-
2018-10-12 16:35:31 -04:00
```javascript
function gcd(a, b) {
if (b == 0)
return a;
else
return gcd(b, (a % b));
}
```
2019-08-07 20:55:02 -03:00
Código C para executar o GCD usando recursão
```c
int gcd(int a, int b)
{
// Everything divides 0
if (a == 0)
return b;
if (b == 0)
return a;
// base case
if (a == b)
return a;
// a is greater
if (a > b)
return gcd(a-b, b);
return gcd(a, b-a);
}
```
Código C ++ para executar o GCD-
```csharp
int gcd(int a,int b) {
int R;
while ((a % b) > 0) {
R = a % b;
a = b;
b = R;
}
return b;
}
```
Código Python para executar o GCD usando recursão
```Python
def gcd(a, b):
if b == 0:
return a:
else:
return gcd(b, (a % b))
```
Código Java para executar o GCD usando recursão
```Java
static int gcd(int a, int b)
{
if(b == 0)
{
return a;
}
return gcd(b, a % b);
}
```
2018-10-12 16:35:31 -04:00
2019-08-07 20:55:02 -03:00
Você também pode usar o Algoritmo Euclidiano para encontrar o GCD de mais de dois números.
Como o GCD é associativo, a seguinte operação é válida - `GCD(a,b,c) == GCD(GCD(a,b), c)`
2018-10-12 16:35:31 -04:00
2019-08-07 20:55:02 -03:00
Calcule o GCD dos dois primeiros números e depois encontre o GCD do resultado e o próximo número.
Exemplo - `GCD(203,91,77) == GCD(GCD(203,91),77) == GCD(7, 77) == 7`
Você pode encontrar GCD de `n` números da mesma maneira.
### Algoritmo Euclideano Estendido
Esta é uma extensão do algoritmo euclidiano. Também calcula os coeficientes x, y tais que
ax+by = gcd(a,b)
x e y são também conhecidos como coeficientes da identidade de Bézout.
Código C para Algoritmo Euclideano Estendido
```c
struct Triplet{
int gcd;
int x;
int y;
};
Triplet gcdExtendedEuclid(int a,int b){
//Base Case
if(b==0){
Triplet myAns;
myAns.gcd = a;
myAns.x = 1;
myAns.y = 0;
return myAns;
}
Triplet smallAns = gcdExtendedEuclid(b,a%b);
//Extended euclid says
Triplet myAns;
myAns.gcd = smallAns.gcd;
myAns.x = smallAns.y;
myAns.y = (smallAns.x - ((a/b)*(smallAns.y)));
return myAns;
}
```