freeCodeCamp/guide/english/mathematics/algebra/piecewise-functions-graphs/index.md

---
title: Piecewise Functions Graphs
---
## Piecewise Functions Graphs

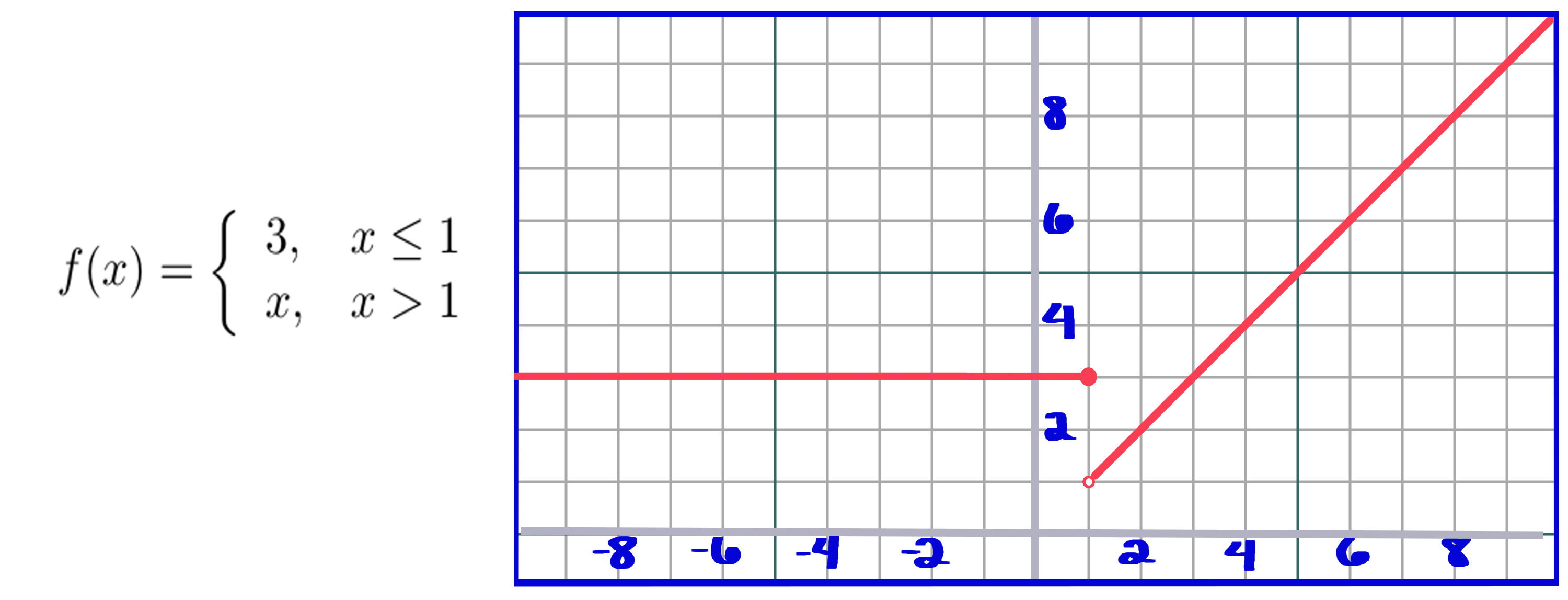
Piecewise functions are defined differently for different intervals of `x`. In order to find `y`, you use `x` to look up what interval it's in. Let's take a look at a simple piecewise function and its graph.

![Piecewise function graph example 1](https://github.com/codersc/freeCodeCamp-article-images/blob/master/art5img1.png?raw=true)

You can see that when `x` is less than or equal to 1, `y` is equal to 3, and when `x` is greater than 1, `y` is equal to x. It's almost like piecewise functions are created by combining different functions into one.

![Piecewise function graph example 2](https://github.com/codersc/freeCodeCamp-article-images/blob/master/art5img2.png?raw=true)

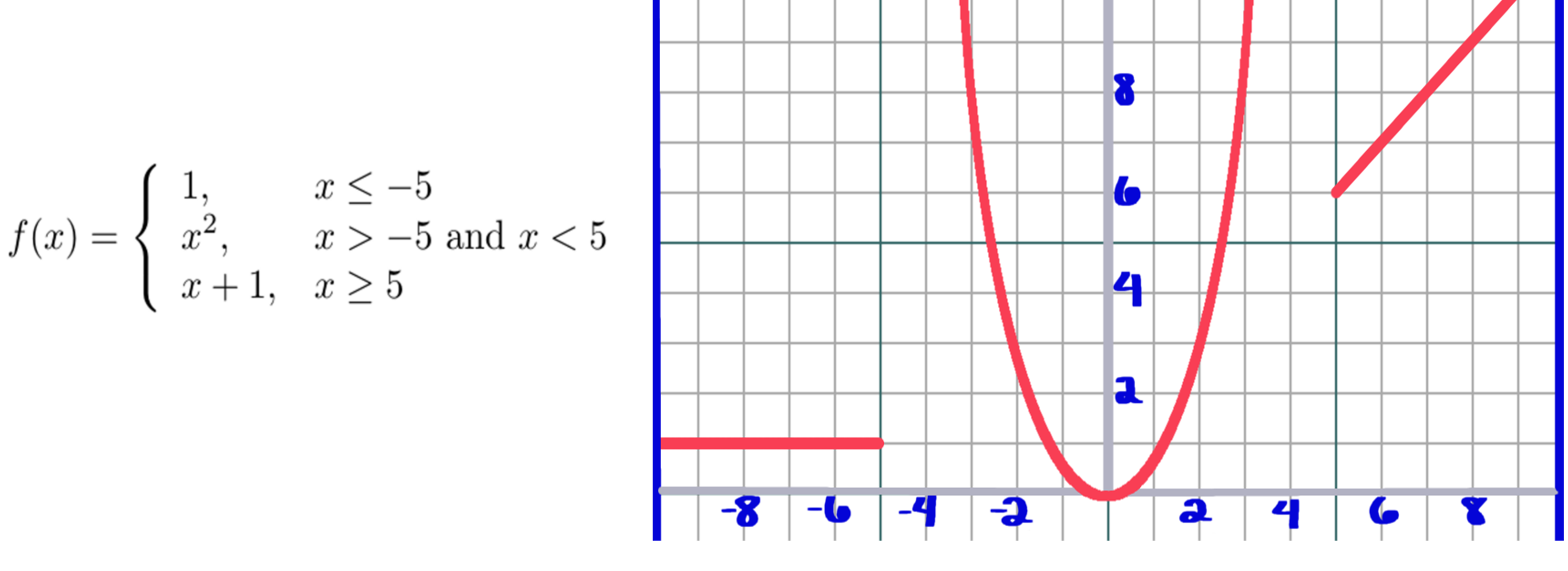
In the graph above you can see that `x` squared could be a standalone function which would be defined for all real numbers. Instead we've defined our piecewise function so only values of `x` that are greater than -5 and less than 5 are input in to `x` squared. Notice that this graph appears to have two "boundary lines" at `x = -5` and `x = 5`, and the first graph has one "boundary line" at `x = 1`.

### Continuous/Non-continuous Piecewise Functions

How can you tell if a particular piecewise function is continuous? Let's look at a couple examples.

![Continuous/Non continuous piecewise functions graphs examples](https://github.com/codersc/freeCodeCamp-article-images/blob/master/art5img3.png?raw=true)