27 lines
1.5 KiB
Markdown
27 lines
1.5 KiB
Markdown
|
|
---
|
||
|
|
title: Orthogonality
|
||
|
|
---
|
||
|
|
## Orthogonality
|
||
|
|
|
||
|
|
In mathematics and linear algebra, two vectors u and v are said to be orthogonal when their dot product is 0:
|
||
|
|
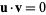
|
||
|
|
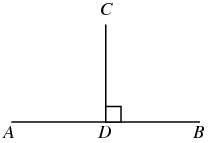
Orthogonality can be thought of as <a href = "http://mathworld.wolfram.com/Perpendicular.html">perpendicularity</a> generalized to higher dimensional vector spaces, since the two are the same- they imply that a right angle is formed by the line, plane, or vector.
|
||
|
|
|
||
|
|
|
||
|
|
|
||
|
|
The following are all examples of orthogonality:
|
||
|
|
1. If two vectors are perpendicular, that is, they meet or intersect at a right (90 degree) angle, they are orthogonal.
|
||
|
|
2. Two vectors are orthogonal if their inner product (dot product) is equal to 0.
|
||
|
|
3. Two vector subspaces A and B in V are orthogonal if every vector in V is orthogonal to every vector in B.
|
||
|
|
|
||
|
|
<!-- <a href='https://github.com/freecodecamp/guides/blob/master/README.md' target='_blank' rel='nofollow'>This quick style guide will help ensure your pull request gets accepted</a>.
|
||
|
|
|
||
|
|
<!-- The article goes here, in GitHub-flavored Markdown. Feel free to add YouTube videos, images, and CodePen/JSBin embeds -->
|
||
|
|
|
||
|
|
#### More Information:
|
||
|
|
1. http://mathworld.wolfram.com/Orthogonal.html
|
||
|
|
2. http://mathworld.wolfram.com/Perpendicular.html
|
||
|
|
<!-- Please add any articles you think might be helpful to read before writing the article -->
|
||
|
|
|
||
|
|
|