2.1 KiB
2.1 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f3fc1000cf542c50ff0e | 問題 143: 三角形のトリチェリ点を調べ上げる | 5 | 301772 | problem-143-investigating-the-torricelli-point-of-a-triangle |
--description--
三角形 ABC は、すべての内角が 120 度未満の三角形です。 三角形内の任意の点を X とし、XA = p, XC = q, XB = r とします。
フェルマーはトリチェリに対し、P + q + r が最小になるような X の位置を見つけるよう挑みました。
トリチェリは、三角形 ABC の各辺に正三角形 AOB, BNC, AMC を作ると、AOB, BNC, AMC の 3 つの外接円が ABC 内の 1 点 T で交わることを証明しました。 さらに、T (トリチェリ-フェルマー点と呼ばれます) が p + q + r を最小化することも証明しました。 さらに驚くべきことに、その和が最小のとき、AN = BM = CO = p + q + r であり、AN, BM, CO も T で交わるということも証明できます。
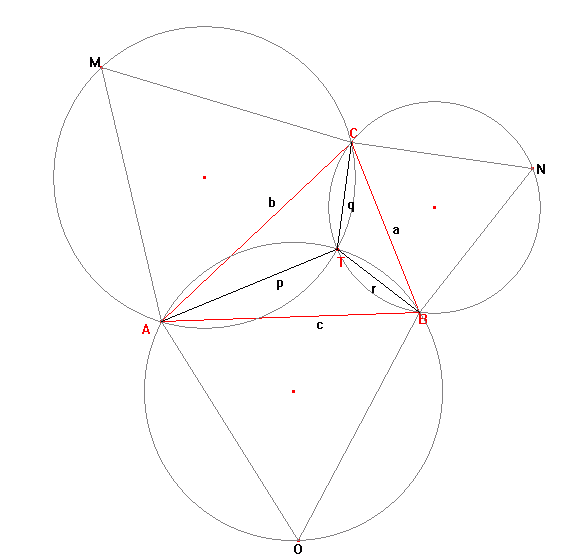
和が最小化され、a, b, c, p, q, r がすべて正の整数である場合、三角形 ABC を「トリチェリ三角形」と呼ぶことにします。 例えば、a = 399, b = 455, c = 511 はトリチェリ三角形の一例であり、p + q + r = 784 です。 トリチェリ三角形について、p + q + r ≤ 120000 の相異なる値の総和を求めなさい。
--hints--
sumTorricelliTriangles() は 30758397 を返す必要があります。
assert.strictEqual(sumTorricelliTriangles(), 30758397);
--seed--
--seed-contents--
function sumTorricelliTriangles() {
return true;
}
sumTorricelliTriangles();
--solutions--
// solution required