2.3 KiB
2.3 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f4031000cf542c50ff15 | 問題 150: 三角配列内で最小和を持つ部分三角形を探す | 5 | 301781 | problem-150-searching-a-triangular-array-for-a-sub-triangle-having-minimum-sum |
--description--
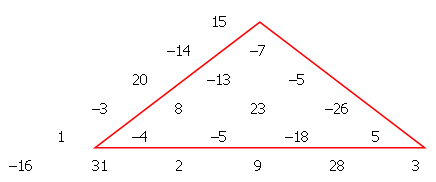
正と負の整数からなる三角配列内で、含まれる数の和が最小である部分三角形を見つけたいとします。
下図の例では、赤で示された三角形がこの条件を -42 で満たしていることを簡単に確認できます。
ここでは 1000 段のそのような三角配列を作りたいので、次のように無作為数生成法 (線形合同法と呼ばれます) によって、値の範囲が ±2^{19} の擬似乱数 s_k を 500500 個生成します。
$$\begin{align} t := & \ 0\\ \ & k = 1\ \text{から}\ k = 500500 \text{ に対して、}:\\ & t := (615949 × t + 797807)\ \text{mod}\ 2^{20}\\ & s_k := t − 219\\ \end{align}$$
したがって、s_1 = 273519, s_2 = -153582, s_3 = 450905 などのようになります。
次のように、疑似乱数からなる三角配列が得られます。
$$ s_1 \\ s_2\;s_3 \\ s_4\; s_5\; s_6 \\ s_7\; s_8\; s_9\; s_{10} \\ \ldots $$
部分三角形は、配列内の任意の要素から開始し、好きなだけ下へ広げることができます (真下の段の 2 要素を次の段から取り、真下の3 要素をさらにその次の段から取り、それ以降も同様にします)。
「部分三角形の和」は、それが含むすべての要素の和として定義されます。
部分三角形の最小和を求めなさい。
--hints--
smallestSubTriangleSum() は -271248680 を返す必要があります。
assert.strictEqual(smallestSubTriangleSum(), -271248680);
--seed--
--seed-contents--
function smallestSubTriangleSum() {
return true;
}
smallestSubTriangleSum();
--solutions--
// solution required