1.7 KiB
1.7 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f4241000cf542c50ff37 | 問題 184: 原点を内包する三角形 | 5 | 301820 | problem-184-triangles-containing-the-origin |
--description--
座標の原点を円心とする半径 r の円に内包される、整数座標を持つ点 (x,y) (すなわち x^2 + y^2 < r^2) の集合 I_r を考えます。
半径が 2 の場合、I_2 には 9 つの点 (0,0), (1,0), (1,1), (0,1), (-1,1), (-1,0), (-1,-1), (0,-1), (1,-1) が含まれます。 原点を内包し、かつ、3 つの頂点がすべて I_2 に含まれるような三角形は 8 つあります。 そのうち 2 つを下図に示します。他の 6 つはこれらを回転すると得られます。
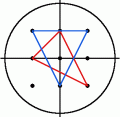
半径が 3 の場合、すべての頂点が I_3 に含まれ、かつ原点を内包するような三角形は 360 個あり、I_5 では 10600 個あります。
3 つ頂点がすべて I_{105} に含まれ、かつ原点を内包するような三角形はいくつありますか。
--hints--
trianglesContainingOrigin() should return 1725323624056.
assert.strictEqual(trianglesContainingOrigin(), 1725323624056);
--seed--
--seed-contents--
function trianglesContainingOrigin() {
return true;
}
trianglesContainingOrigin();
--solutions--
// solution required