1.8 KiB
1.8 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f4691000cf542c50ff7b | 問題 252: 凸状の穴 | 5 | 301900 | problem-252-convex-holes |
--description--
平面上の点の集合が与えられたとき、「凸状の穴」とは、与えられた点のいずれかを頂点とし、与えられた点のいずれもその内部に含まない凸多角形であると定義します (与えられた点が、多角形の頂点だけでなく辺上にもあって良い)。
一例として、20 個の点の集合と、上で定義した凸状の穴を下図にいくつか示します。 赤の多角形で示されている凸状の穴は、面積が 1049694.5 平方単位であり、これらの点の集合で作られる最大の凸状の穴です。
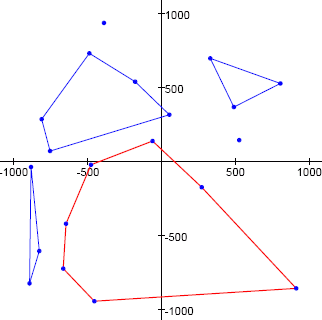
この例では、次の擬似乱数法によって生成された最初の 20 個の点 (T_{2k − 1}, T_{2k}) (ここで k = 1, 2, \ldots, 20) を使用しました。
$$\begin{align} S_0 & = 290\,797 \\ S_{n+1} & = {S_n}^2 \; \text{mod} \; 50\,515\,093 \\ T_n & = (S_n \; \text{mod} \; 2000) − 1000 \end{align}$$
すなわち、(527, 144), (−488, 732), (−454, −947), …です。
この擬似乱数列の最初の 500 個の点で作られる凸状の穴について、その最大面積を求めなさい。 回答は、小数第 1 位まで示すこと。
--hints--
convexHoles() は 104924 を返す必要があります。
assert.strictEqual(convexHoles(), 104924);
--seed--
--seed-contents--
function convexHoles() {
return true;
}
convexHoles();
--solutions--
// solution required