Files

camperbot 43a2a0a395 chore(i18n,learn): processed translations (#44866 )

2022-01-23 00:08:20 +09:00

2.6 KiB

Raw Permalink Blame History

id, title, challengeType, forumTopicId, dashedName

id	title	challengeType	forumTopicId	dashedName
5900f46c1000cf542c50ff7e	問題 256: 畳を敷けない部屋	5	301904	problem-256-tatami-free-rooms

--description--

畳のような長方形のマットを、部屋の床の上に互いに重ねることなく敷き詰める場合を考えます。

サイズが 1 × 2 の畳しかないと仮定すると、当然、その畳で敷き詰めることのできる部屋の形やサイズには制限があります。

この問題では、整数寸法 a と $b$、および偶数サイズ s = a \times b を持つ長方形の部屋のみを考えます。ここで、「サイズ」は部屋の床面積を表します。また、一般性を失うことなく、a ≤ b という条件を加えます。

畳を敷くときは 1 つのルールがあります。4 枚の畳の角が 1 ヵ所に集まってはいけないのです。例えば、4 × 4 の部屋を次の 2 通りで敷くことを考えます。

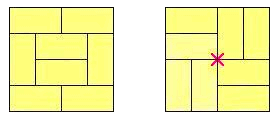
左側の配置は問題ありませんが、右側の配置はルールに反しています。中央の赤い印 "X" は、4 枚の畳の角が集まっている個所を示しています。

このルールにより、ある偶数サイズの部屋は畳を敷き詰めることができません。そのような部屋を「畳を敷けない部屋」と呼ぶことにします。さらに、サイズが s である「畳を敷けない部屋」の数を T(s) とします。

最小の「畳を敷けない部屋」はサイズが $s = 70$、寸法が 7ｘ10 です。サイズ s = 70 である他のすべての部屋 (1×70, 2×35, 5×14) には畳を敷き詰めることができます。したがって、T(70) = 1 です。

同様に、サイズが s = 1320 である「畳を敷けない部屋」はちょうど 5 つあるので (20×66, 22×60, 24×55, 30×44, 33x40)、T(1320) = 5 であることを確認できます。実は s = 1320 は、T(s) = 5 である最小の部屋のサイズ s です。

T(s) = 200 である最小の部屋のサイズ s を求めなさい。

--hints--

tatamiFreeRooms() は 85765680 を返す必要があります。

assert.strictEqual(tatamiFreeRooms(), 85765680);

--seed--

--seed-contents--

function tatamiFreeRooms() {

  return true;
}

tatamiFreeRooms();

--solutions--

// solution required

2.6 KiB Raw Permalink Blame History Unescape Escape