1.7 KiB
1.7 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f4751000cf542c50ff87 | 問題 264: 三角形の中心 | 5 | 301913 | problem-264-triangle-centres |
--description--
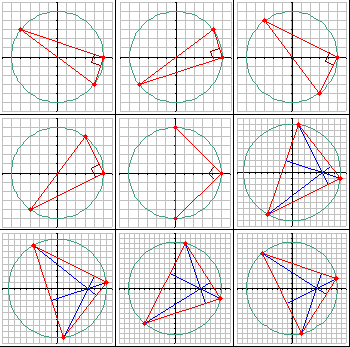
以下が当てはまるすべての三角形について考えてます。
- すべての頂点が格子点上にある。
- 外心が原点 O にある。
- 垂心が点 H (5, 0) にある。
\text{周長} ≤ 50 に対してこのような三角形は 9 つあります。
それらを下表に周長の昇順で示します。
|
A(-4, 3), B(5, 0), C(4, -3) A(4, 3), B(5, 0), C(-4, -3) A(-3, 4), B(5, 0), C(3, -4) A(3, 4), B(5, 0), C(-3, -4) A(0, 5), B(5, 0), C(0, -5) A(1, 8), B(8, -1), C(-4, -7) A(8, 1), B(1, -8), C(-4, 7) A(2, 9), B(9, -2), C(-6, -7) A(9, 2), B(2, -9), C(-6, 7) |
 |
これらの周長の和を小数第 4 位に四捨五入すると 291.0089 です。
\text{周長} ≤ {10}^5 を満たすこのような三角形をすべて求めなさい。 回答は、これらの三角形の周長の和を四捨五入して小数第 4 位まで示すこと。
--hints--
triangleCentres() は 2816417.1055 を返す必要があります。
assert.strictEqual(triangleCentres(), 2816417.1055);
--seed--
--seed-contents--
function triangleCentres() {
return true;
}
triangleCentres();
--solutions--
// solution required