freeCodeCamp/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-287-quadtree-encoding-a-simple-compression-algorithm.md

id, title, challengeType, forumTopicId, dashedName

id	title	challengeType	forumTopicId	dashedName
5900f48b1000cf542c50ff9e	問題 287: 四分木符号化 (単純な圧縮アルゴリズム)	5	301938	problem-287-quadtree-encoding-a-simple-compression-algorithm

--description--

四分木符号化により、2^N×2^N の白黒画像をビット (0, 1) 列で表すことができます。 このビット列は、左から右へ次のように解釈されます。

• 最初のビットは 2^N×2^N の領域全体を表します。
• "0" は分割を意味します。
  • 現在の 2^n×2^n の領域は、寸法 2^{n - 1}×2^{n - 1} の 4 つの部分領域に分割されます。
  • 次のビットには、左上、右上、左下、右下の部分領域の説明がこの順序で含まれています。
• "10" は、現在の領域が黒いピクセルのみを含んでいることを示します。
• "11" は、現在の領域が白いピクセルのみを含んでいることを示します。

次の 4×4 の画像について考えます (色付きのマークは分割可能な場所を示します)。

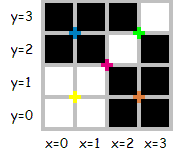
この画像は、例えば次のようにいくつかの数列で表すことができます。"001010101001011111011010101010" (長さ 30)、または "0100101111101110" (長さ 16、この画像での最小数列)

正の整数 N に対し、次のように色が付く 2^N×2^N の画像をD_N とします。

• 座標 x = 0, y = 0 のピクセルは左下のピクセルに対応します。
• {(x - 2^{N - 1})}^2 + {(y - 2 ^{N - 1})}^2 = 2^{2N - 2} の場合、ピクセルは黒です。
• それ以外の場合、ピクセルは白です。

D_{24} を表す最小の数列の長さを求めなさい。

--hints--

quadtreeEncoding() は 313135496 を返す必要があります。

assert.strictEqual(quadtreeEncoding(), 313135496);

--seed--

--seed-contents--

function quadtreeEncoding() {

  return true;
}

quadtreeEncoding();

--solutions--

// solution required