2.1 KiB
2.1 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f4971000cf542c50ffaa | 問題 299: 3 つの相似三角形 | 5 | 301951 | problem-299-three-similar-triangles |
--description--
整数座標を持つ、次の 4 つの点が選択されます。
A(a, 0), B(b, 0), C(0, c), D(0, d) (0 < a < b かつ 0 < c < d)
3 つの三角形 ABP, CDP, BDP がすべて相似形になるように、同じく整数座標を持つ点 P を線 AC 上で選びます。
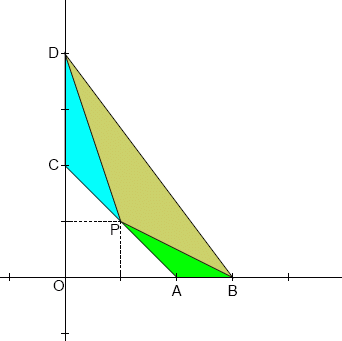
a = c のときのみ 3 つの三角形が相似形になり得るということは、容易に証明できます。
つまり、a=c とすると、(整数座標を持つ) 点 P が AC 上に少なくとも 1 つ存在して 3 つの三角形 ABP, CDP, BDP がすべて相似形になるような、三つ組数 (a, b, d) を探します。
例えば、(a, b, d) = (2, 3, 4) の場合、点 P(1, 1) が上の条件を満たすことを容易に確認できます。 注意点として、三つ組数 (2,3,4) と (2,4,3) は点 P(1, 1) を共有しますが相異なる組とみなされます。
b + d < 100 の場合、点 P が存在するような相異なる三つ組数 (a, b, d) は 92 個存在します。
b + d < 100\\,000 の場合、点 P が存在するような相異なる三つ組数 (a, b, d) は 320471 個存在します。
b + d < 100\\,000\\,000 の場合、点 P が存在するような相異なる三つ組数 (a, b, d) はいくつ存在しますか。
--hints--
threeSimilarTriangles() は 549936643 を返す必要があります。
assert.strictEqual(threeSimilarTriangles(), 549936643);
--seed--
--seed-contents--
function threeSimilarTriangles() {
return true;
}
threeSimilarTriangles();
--solutions--
// solution required