1.9 KiB
1.9 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f49f1000cf542c50ffb1 | 問題 306: 短冊ゲーム | 5 | 301960 | problem-306-paper-strip-game |
--description--
次のゲームは、組み合わせゲーム理論の古典的な例です。
一列に並べた n 個の白いマスが最初にあり、2 人のプレイヤーが交互にプレイしていきます。 それぞれのターンで、プレイヤーは連続する白いマスを 2 つ選び、それらを黒く塗ります。 先にどこも塗れなくなったプレイヤーの負けです。
n = 1: 有効な塗り方がないため、先手が自動的に負けます。n = 2: 有効な塗り方は 1 通りのみです。その後、後手が負けます。n = 3: 有効な塗り方が 2 通りありますが、いずれでも後手が負けます。n = 4: 先手には 3 通りの有効な塗り方があります。中央の 2 マスを塗れば勝てます。n = 5: 先手には有効な塗り方が 4 通りありますが (下図の赤色)、いずれでも後手 (青) が勝ちます。
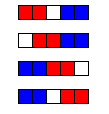
したがって、1 ≤ n ≤ 5 のとき、先手が必ず勝てるような n の値は 3 つあります。
同様に、1 ≤ n ≤ 50 のとき、先手が必ず勝てるような n の値は 40 個あります。
1 ≤ n ≤ 1\\,000\\,000 のとき、先手が必ず勝てるような n の値はいつくありますか。
--hints--
paperStripGame() は 852938 を返す必要があります。
assert.strictEqual(paperStripGame(), 852938);
--seed--
--seed-contents--
function paperStripGame() {
return true;
}
paperStripGame();
--solutions--
// solution required