Files

camperbot 43a2a0a395 chore(i18n,learn): processed translations (#44866 )

2022-01-23 00:08:20 +09:00

id, title, challengeType, forumTopicId, dashedName

id	title	challengeType	forumTopicId	dashedName
5900f4a31000cf542c50ffb6	問題 311: 二斜整数四辺形	5	301967	problem-311-biclinic-integral-quadrilaterals

--description--

四角形 ABCD は、1 ≤ AB < BC < CD < AD かつ辺長が整数である凸四角形です。

BD の長さは整数です。 O は BD の中点です。 AO の長さは整数です。

AO = CO ≤ BO = DO の場合、ABCD を「二斜整数四辺形」(biclinic integral quadrilateral) と呼ぶことにします。

例えば、下の四辺形は AB = 19, BC = 29, CD = 37, AD = 43, BD = 48, AO = CO = 23 であり、二斜整数四角形です。

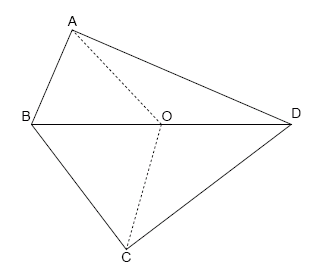
{AB}^2 + {BC}^2 + {CD}^2 + {AD}^2 ≤ N を満たす相異なる二斜整数四角形 ABCD の数を、B(N) とします。 B(10\\000) = 49, B(1\\,000\\000) = 38239 であることを確認できます。

B(10\\,000\\,000\\,000) を求めなさい。

--hints--

biclinicIntegralQuadrilaterals() は 2466018557 を返す必要があります。

assert.strictEqual(biclinicIntegralQuadrilaterals(), 2466018557);

function biclinicIntegralQuadrilaterals() {

  return true;
}

biclinicIntegralQuadrilaterals();

// solution required