1.5 KiB
1.5 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f5081000cf542c510019 | 問題 411: 登り坂を描く経路 | 5 | 302080 | problem-411-uphill-paths |
--description--
n を正の整数とします。 0 ≤ i ≤ 2n のとき、座標 (x, y) = (2^i\bmod n, 3^i\bmod n) に駅があるとします。 同じ座標を持つ駅が複数ある場合、それらは同じ駅であると考えます。
x, y 座標の値が減少することのない経路を、(0, 0) から (n, n) まで作成するとします。
その経路が通過できる駅の最大数を S(n) とします。
例えば、n = 22 のとき、11 の相異なる駅があり、1 本の有効な経路がたかだか 5 駅を通ることができます。 したがって、S(22) = 5 となります。 下図に、このケースを最適な経路の例と共に示します。
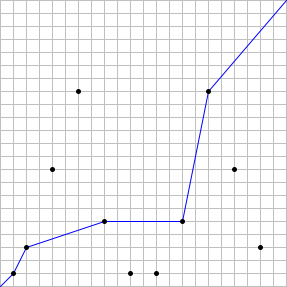
S(123) = 14, S(10\\,000) = 48 であることも確認できます。
1 ≤ k ≤ 30 のとき、\sum S(k^5) を求めなさい。
--hints--
uphillPaths() は 9936352 を返す必要があります。
assert.strictEqual(uphillPaths(), 9936352);
--seed--
--seed-contents--
function uphillPaths() {
return true;
}
uphillPaths();
--solutions--
// solution required