2.0 KiB
2.0 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f5191000cf542c51002b | 問題 428: 円のネックレス | 5 | 302098 | problem-428-necklace-of-circles |
--description--
a, b, c を正の数とします。
|WX| = a, |XY| = b, |YZ| = c, |WZ| = a + b + c となる同一直線上の 4 点 を W, X, Y, Z とします。
直径が XY である円を C_{\text{in}} とします。
直径が WZ である円を C_{\text{out}} とします。
k (≥ 3) 個の相異なる円 C_1, C_2, \ldots, C_k を、以下の条件をすべて満たすように配置できる場合、三つ組数 (a, b, c) はネックレス三つ組数と呼ばれます。
C_iは、1 ≤ i,j ≤ kかつi ≠ jのとき、いずれのC_jとも内点を共有しない。C_iは、1 ≤ i ≤ kのとき、C_{\text{in}}およびC_{\text{out}}の両方に接している。C_iは、1 ≤ i < kのとき、C_{i + 1}に接している。C_kはC_1に接している。
例えば、(5, 5, 5) と (4, 3, 21) はネックレス三つ組数です。しかし、(2, 2, 5) はそうではないことが分かっています。
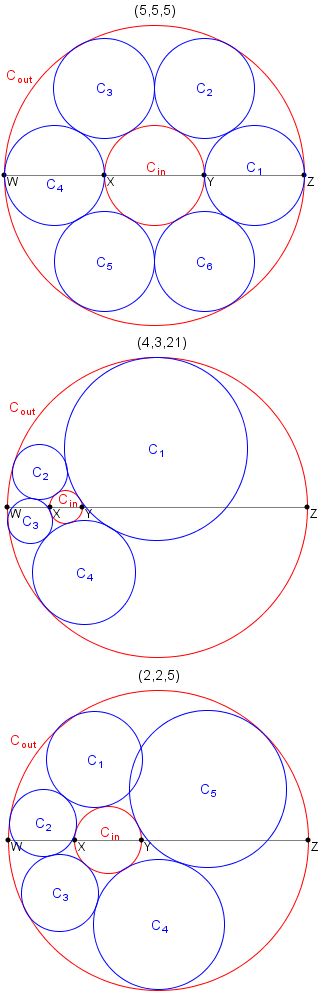
a, b, c が正の整数で、かつ b ≤ n のときのネックレス三つ組数の個数を T(n) とします。 例えば、T(1) = 9, T(20) = 732, T(3\\,000) = 438\\,106 です。
T(1\\,000\\,000\\,000) を求めなさい。
--hints--
necklace(1000000000) は 747215561862 を返す必要があります。
assert.strictEqual(necklace(1000000000), 747215561862);
--seed--
--seed-contents--
function necklace(n) {
return true;
}
necklace(1000000000)
--solutions--
// solution required