freeCodeCamp/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-86-cuboid-route.md

id, title, challengeType, forumTopicId, dashedName

id	title	challengeType	forumTopicId	dashedName
5900f3c31000cf542c50fed5	問題 86: 直方体の経路	5	302200	problem-86-cuboid-route

--description--

寸法 6 × 5 × 3 の直方体の部屋の一方の角にクモ S、反対側の角にハエ F がいます。 部屋の表面を移動するとして、S から F までの最短の「直線」距離は 10 です。その経路が図に示されています。

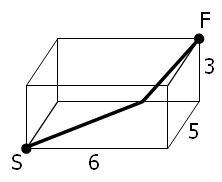
しかし、任意の直方体に対して「最短」経路の候補は最大 3 本あります。最短経路の長さが整数であるとは限りません。

M = 100 のとき、最短経路の長さが整数かつ寸法が整数 (最大寸法 M x M x M) である相異なる直方体は、回転を無視すればちょうど 2060 個存在することが分かっています。 これは、解が 2000 個を超える最初の M 値です。M = 99 では解が 1975 個あります。

解の個数が n を超える最初の M を求めなさい。

--hints--

cuboidRoute(2000) は数値を返す必要があります。

assert(typeof cuboidRoute(2000) === 'number');

cuboidRoute(2000) は 100 を返す必要があります。

assert.strictEqual(cuboidRoute(2000), 100);

cuboidRoute(25000) は 320 を返す必要があります。

assert.strictEqual(cuboidRoute(25000), 320);

cuboidRoute(500000) は 1309 を返す必要があります。

assert.strictEqual(cuboidRoute(500000), 1309);

cuboidRoute(1000000) は 1818 を返す必要があります。

assert.strictEqual(cuboidRoute(1000000), 1818);

--seed--

--seed-contents--

function cuboidRoute(n) {

  return true;
}

cuboidRoute(2000);

--solutions--

function cuboidRoute(n) {
  // Based on https://www.mathblog.dk/project-euler-86-shortest-path-cuboid/
  function getLength(a, b) {
    return Math.sqrt(a ** 2 + b ** 2);
  }

  let M = 2;
  let counter = 0;

  while (counter < n) {
    M++;
    for (let baseHeightWidth = 3; baseHeightWidth <= 2 * M; baseHeightWidth++) {
      const pathLength = getLength(M, baseHeightWidth);
      if (Number.isInteger(pathLength)) {
        if (baseHeightWidth <= M) {
          counter += Math.floor(baseHeightWidth / 2);
        } else {
          counter += 1 + M - Math.floor((baseHeightWidth + 1) / 2);
        }
      }
    }
  }

  return M;
}