* fix: clean-up Project Euler 141-160 * fix: corrections from review Co-authored-by: Sem Bauke <46919888+Sembauke@users.noreply.github.com> * fix: corrections from review Co-authored-by: Tom <20648924+moT01@users.noreply.github.com> * fix: use different notation for consistency * Update curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-144-investigating-multiple-reflections-of-a-laser-beam.md Co-authored-by: gikf <60067306+gikf@users.noreply.github.com> Co-authored-by: Sem Bauke <46919888+Sembauke@users.noreply.github.com> Co-authored-by: Tom <20648924+moT01@users.noreply.github.com>
1.5 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f3ff1000cf542c50ff12 | Problem 147: Rectangles in cross-hatched grids | 5 | 301776 | problem-147-rectangles-in-cross-hatched-grids |
--description--
In a 3x2 cross-hatched grid, a total of 37 different rectangles could be situated within that grid as indicated in the sketch.
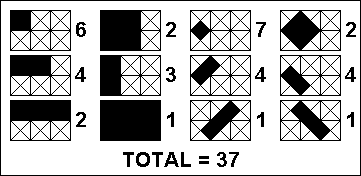
There are 5 grids smaller than 3x2, vertical and horizontal dimensions being important, i.e. 1x1, 2x1, 3x1, 1x2 and 2x2. If each of them is cross-hatched, the following number of different rectangles could be situated within those smaller grids:
$$\begin{array}{|c|c|} \hline 1 \times 1 & 1 \\ \hline 2 \times 1 & 4 \\ \hline 3 \times 1 & 8 \\ \hline 1 \times 2 & 4 \\ \hline 2 \times 2 & 18 \\ \hline \end{array}$$
Adding those to the 37 of the 3x2 grid, a total of 72 different rectangles could be situated within 3x2 and smaller grids.
How many different rectangles could be situated within 47x43 and smaller grids?
--hints--
crossHatchedRectangles() should return 846910284.
assert.strictEqual(crossHatchedRectangles(), 846910284);
--seed--
--seed-contents--
function crossHatchedRectangles() {
return true;
}
crossHatchedRectangles();
--solutions--
// solution required