freeCodeCamp/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-155-counting-capacitor-circuits.md

id, title, challengeType, forumTopicId, dashedName

id	title	challengeType	forumTopicId	dashedName
5900f4081000cf542c50ff1a	Problem 155: Counting Capacitor Circuits	5	301786	problem-155-counting-capacitor-circuits

--description--

An electric circuit uses exclusively identical capacitors of the same value C.

The capacitors can be connected in series or in parallel to form sub-units, which can then be connected in series or in parallel with other capacitors or other sub-units to form larger sub-units, and so on up to a final circuit.

Using this simple procedure and up to n identical capacitors, we can make circuits having a range of different total capacitances. For example, using up to n = 3 capacitors of 60 μF each, we can obtain the following 7 distinct total capacitance values:

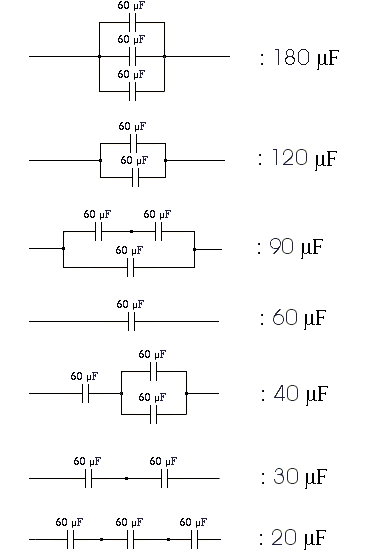
If we denote by D(n) the number of distinct total capacitance values we can obtain when using up to n equal-valued capacitors and the simple procedure described above, we have: D(1) = 1, D(2) = 3, D(3)=7, \ldots

Find D(18).

Reminder: When connecting capacitors C_1, C_2 etc in parallel, the total capacitance is C_T = C_1 + C_2 + \cdots, whereas when connecting them in series, the overall capacitance is given by: \frac{1}{C_T} = \frac{1}{C_1} + \frac{1}{C_2} + \cdots.

--hints--

capacitanceValues() should return 3857447.

assert.strictEqual(capacitanceValues(), 3857447);

--seed--

--seed-contents--

function capacitanceValues() {

  return true;
}

capacitanceValues();

--solutions--

// solution required