* fix: clean-up Project Euler 161-180 * fix: corrections from review Co-authored-by: Tom <20648924+moT01@users.noreply.github.com> Co-authored-by: Tom <20648924+moT01@users.noreply.github.com>
1.6 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f40f1000cf542c50ff22 | Problem 163: Cross-hatched triangles | 5 | 301797 | problem-163-cross-hatched-triangles |
--description--
Consider an equilateral triangle in which straight lines are drawn from each vertex to the middle of the opposite side, such as in the size 1 triangle in the sketch below.
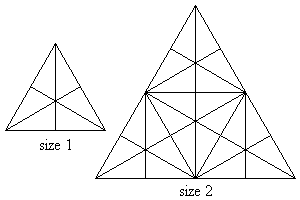
Sixteen triangles of either different shape or size or orientation or location can now be observed in that triangle. Using size 1 triangles as building blocks, larger triangles can be formed, such as the size 2 triangle in the above sketch. One-hundred and four triangles of either different shape or size or orientation or location can now be observed in that size 2 triangle.
It can be observed that the size 2 triangle contains 4 size 1 triangle building blocks. A size 3 triangle would contain 9 size 1 triangle building blocks and a size n triangle would thus contain n^2 size 1 triangle building blocks.
If we denote T(n) as the number of triangles present in a triangle of size n, then
$$\begin{align} & T(1) = 16 \\ & T(2) = 104 \end{align}$$
Find T(36).
--hints--
crossHatchedTriangles() should return 343047.
assert.strictEqual(crossHatchedTriangles(), 343047);
--seed--
--seed-contents--
function crossHatchedTriangles() {
return true;
}
crossHatchedTriangles();
--solutions--
// solution required