* fix: clean-up Project Euler 281-300 * fix: missing image extension * fix: missing power Co-authored-by: Tom <20648924+moT01@users.noreply.github.com> * fix: missing subscript Co-authored-by: Tom <20648924+moT01@users.noreply.github.com> Co-authored-by: Tom <20648924+moT01@users.noreply.github.com>
1.5 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f48d1000cf542c50ffa0 | Problem 289: Eulerian Cycles | 5 | 301940 | problem-289-eulerian-cycles |
--description--
Let C(x,y) be a circle passing through the points (x, y), (x, y + 1), (x + 1, y) and (x + 1, y + 1).
For positive integers m and n, let E(m,n) be a configuration which consists of the m·n circles: { C(x,y): 0 ≤ x < m, 0 ≤ y < n, x and y are integers }
An Eulerian cycle on E(m,n) is a closed path that passes through each arc exactly once. Many such paths are possible on E(m,n), but we are only interested in those which are not self-crossing: A non-crossing path just touches itself at lattice points, but it never crosses itself.
The image below shows E(3,3) and an example of an Eulerian non-crossing path.
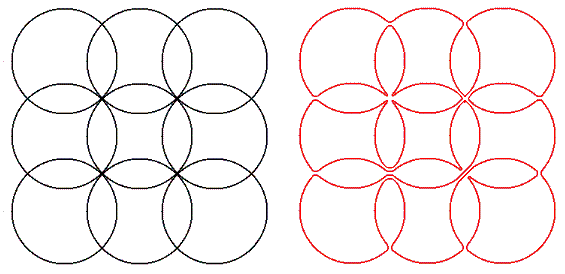
Let L(m,n) be the number of Eulerian non-crossing paths on E(m,n). For example, L(1,2) = 2, L(2,2) = 37 and L(3,3) = 104290.
Find L(6,10)\bmod {10}^{10}.
--hints--
eulerianCycles() should return 6567944538.
assert.strictEqual(eulerianCycles(), 6567944538);
--seed--
--seed-contents--
function eulerianCycles() {
return true;
}
eulerianCycles();
--solutions--
// solution required