1.7 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f4b71000cf542c50ffca | Problem 331: Cross flips | 5 | 301989 | problem-331-cross-flips |
--description--
N×N disks are placed on a square game board. Each disk has a black side and white side.
At each turn, you may choose a disk and flip all the disks in the same row and the same column as this disk: thus 2 × N - 1 disks are flipped. The game ends when all disks show their white side. The following example shows a game on a 5×5 board.
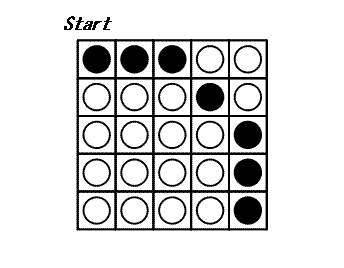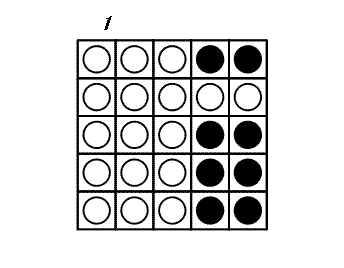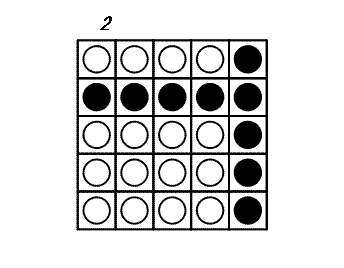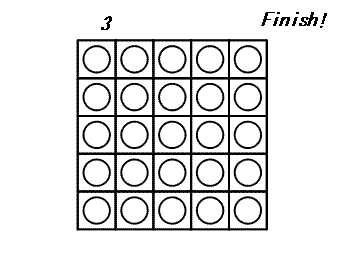
It can be proven that 3 is the minimal number of turns to finish this game.
The bottom left disk on the N×N board has coordinates (0, 0); the bottom right disk has coordinates (N - 1,$0$) and the top left disk has coordinates (0,$N - 1$).
Let C_N be the following configuration of a board with N × N disks: A disk at (x, y) satisfying N - 1 \le \sqrt{x^2 + y^2} \lt N, shows its black side; otherwise, it shows its white side. C_5 is shown above.
Let T(N) be the minimal number of turns to finish a game starting from configuration C_N or 0 if configuration C_N is unsolvable. We have shown that T(5) = 3. You are also given that T(10) = 29 and T(1\\,000) = 395\\,253.
Find \displaystyle \sum_{i = 3}^{31} T(2^i - i).
--hints--
crossFlips() should return 467178235146843500.
assert.strictEqual(crossFlips(), 467178235146843500);
--seed--
--seed-contents--
function crossFlips() {
return true;
}
crossFlips();
--solutions--
// solution required