freeCodeCamp/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-334-spilling-the-beans.md

id, title, challengeType, forumTopicId, dashedName

id	title	challengeType	forumTopicId	dashedName
5900f4ba1000cf542c50ffcd	Problem 334: Spilling the beans	5	301992	problem-334-spilling-the-beans

--description--

In Plato's heaven, there exist an infinite number of bowls in a straight line. Each bowl either contains some or none of a finite number of beans. A child plays a game, which allows only one kind of move: removing two beans from any bowl, and putting one in each of the two adjacent bowls. The game ends when each bowl contains either one or no beans.

For example, consider two adjacent bowls containing 2 and 3 beans respectively, all other bowls being empty. The following eight moves will finish the game:

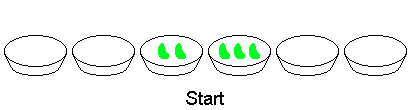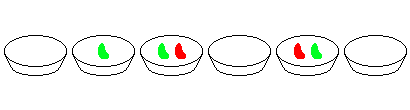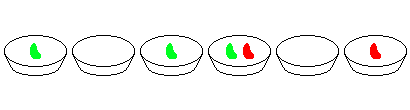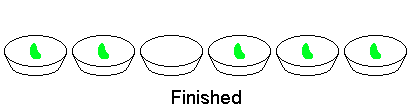
You are given the following sequences:

$$\begin{align} & t_0 = 123456, \\ & t_i = \begin{cases} \frac{t_{i - 1}}{2}, & \text{if t_{i - 1} is even} \\ \left\lfloor\frac{t_{i - 1}}{2}\right\rfloor \oplus 926252, & \text{if t_{i - 1} is odd} \end{cases} \\ & \qquad \text{where ⌊x⌋ is the floor function and \oplus is the bitwise XOR operator.} \\ & b_i = (t_i\bmod 2^{11}) + 1. \end{align}$$

The first two terms of the last sequence are b_1 = 289 and b_2 = 145. If we start with b_1 and b_2 beans in two adjacent bowls, 3419100 moves would be required to finish the game.

Consider now 1500 adjacent bowls containing b_1, b_2, \ldots, b_{1500} beans respectively, all other bowls being empty. Find how many moves it takes before the game ends.

--hints--

spillingTheBeans() should return 150320021261690850.

assert.strictEqual(spillingTheBeans(), 150320021261690850);

--seed--

--seed-contents--

function spillingTheBeans() {

  return true;
}

spillingTheBeans();

--solutions--

// solution required