freeCodeCamp/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-354-distances-in-a-bees-honeycomb.md

id, title, challengeType, forumTopicId, dashedName

id	title	challengeType	forumTopicId	dashedName
5900f4cf1000cf542c50ffe1	Problem 354: Distances in a bee's honeycomb	5	302014	problem-354-distances-in-a-bees-honeycomb

--description--

Consider a honey bee's honeycomb where each cell is a perfect regular hexagon with side length 1.

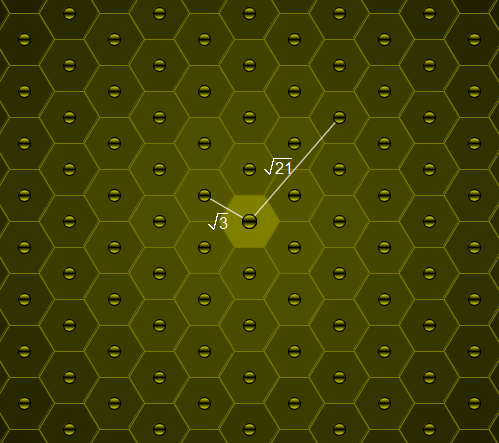
One particular cell is occupied by the queen bee. For a positive real number L, let B(L) count the cells with distance L from the queen bee cell (all distances are measured from centre to centre); you may assume that the honeycomb is large enough to accommodate for any distance we wish to consider.

For example, B(\sqrt{3}) = 6, B(\sqrt{21}) = 12 and B(111\\,111\\,111) = 54.

Find the number of L ≤ 5 \times {10}^{11} such that B(L) = 450.

--hints--

distancesInHoneycomb() should return 58065134.

assert.strictEqual(distancesInHoneycomb(), 58065134);

--seed--

--seed-contents--

function distancesInHoneycomb() {

  return true;
}

distancesInHoneycomb();

--solutions--

// solution required