freeCodeCamp/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-411-uphill-paths.md

id, title, challengeType, forumTopicId, dashedName

id	title	challengeType	forumTopicId	dashedName
5900f5081000cf542c510019	Problem 411: Uphill paths	5	302080	problem-411-uphill-paths

--description--

Let n be a positive integer. Suppose there are stations at the coordinates (x, y) = (2^i\bmod n, 3^i\bmod n) for 0 ≤ i ≤ 2n. We will consider stations with the same coordinates as the same station.

We wish to form a path from (0, 0) to (n, n) such that the x and y coordinates never decrease.

Let S(n) be the maximum number of stations such a path can pass through.

For example, if n = 22, there are 11 distinct stations, and a valid path can pass through at most 5 stations. Therefore, S(22) = 5. The case is illustrated below, with an example of an optimal path:

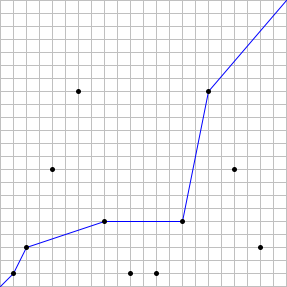
It can also be verified that S(123) = 14 and S(10\\,000) = 48.

Find \sum S(k^5) for 1 ≤ k ≤ 30.

--hints--

uphillPaths() should return 9936352.

assert.strictEqual(uphillPaths(), 9936352);

--seed--

--seed-contents--

function uphillPaths() {

  return true;
}

uphillPaths();

--solutions--

// solution required