freeCodeCamp/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-422-sequence-of-points-on-a-hyperbola.md

id, title, challengeType, forumTopicId, dashedName

id	title	challengeType	forumTopicId	dashedName
5900f5131000cf542c510025	Problem 422: Sequence of points on a hyperbola	5	302092	problem-422-sequence-of-points-on-a-hyperbola

--description--

Let H be the hyperbola defined by the equation 12x^2 + 7xy - 12y^2 = 625.

Next, define X as the point (7, 1). It can be seen that X is in H.

Now we define a sequence of points in H, \\{P_i : i ≥ 1\\}, as:

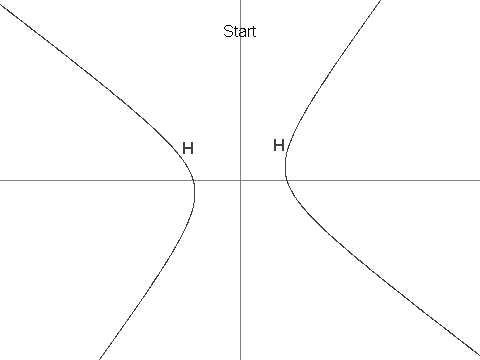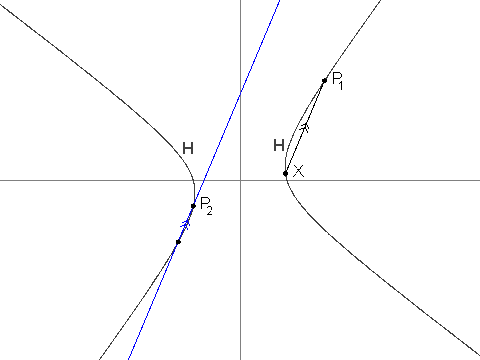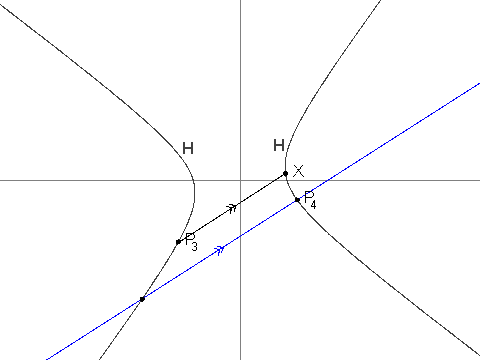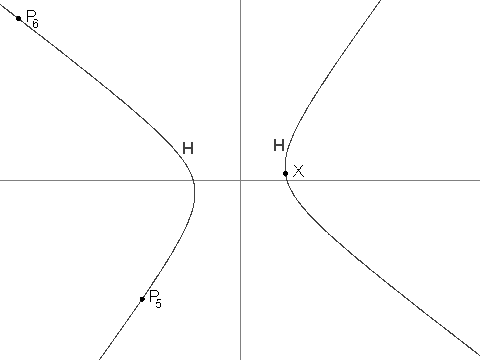
• P_1 = (13, \frac{61}{4}).
• P_2 = (\frac{-43}{6}, -4).
• For i > 2, P_i is the unique point in H that is different from P_{i - 1} and such that line P_iP_{i - 1} is parallel to line P_{i - 2}X. It can be shown that P_i is well-defined, and that its coordinates are always rational.

You are given that P_3 = (\frac{-19}{2}, \frac{-229}{24}), P_4 = (\frac{1267}{144}, \frac{-37}{12}) and P_7 = (\frac{17\\,194\\,218\\,091}{143\\,327\\,232}, \frac{274\\,748\\,766\\,781}{1\\,719\\,926\\,784}).

Find P_n for n = {11}^{14} in the following format: If P_n = (\frac{a}{b}, \frac{c}{d}) where the fractions are in lowest terms and the denominators are positive, then the answer is (a + b + c + d)\bmod 1\\,000\\,000\\,007.

For n = 7, the answer would have been: 806\\,236\\,837.

--hints--

sequenceOfPointsOnHyperbola() should return 92060460.

assert.strictEqual(sequenceOfPointsOnHyperbola(), 92060460);

--seed--

--seed-contents--

function sequenceOfPointsOnHyperbola() {

  return true;
}

sequenceOfPointsOnHyperbola();

--solutions--

// solution required