freeCodeCamp/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-86-cuboid-route.md

id, title, challengeType, forumTopicId, dashedName

id	title	challengeType	forumTopicId	dashedName
5900f3c31000cf542c50fed5	Problem 86: Cuboid route	5	302200	problem-86-cuboid-route

--description--

A spider, S, sits in one corner of a cuboid room, measuring 6 by 5 by 3, and a fly, F, sits in the opposite corner. By travelling on the surfaces of the room the shortest "straight line" distance from S to F is 10 and the path is shown on the diagram.

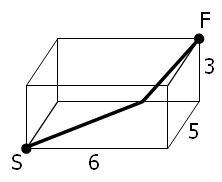
However, there are up to three "shortest" path candidates for any given cuboid and the shortest route doesn't always have integer length.

It can be shown that there are exactly 2060 distinct cuboids, ignoring rotations, with integer dimensions, up to a maximum size of M by M by M, for which the shortest route has integer length when M = 100. This is the least value of M for which the number of solutions first exceeds two thousand; the number of solutions when M = 99 is 1975.

Find the least value of M such that the number of solutions first exceeds n.

--hints--

cuboidRoute(2000) should return a number.

assert(typeof cuboidRoute(2000) === 'number');

cuboidRoute(2000) should return 100.

assert.strictEqual(cuboidRoute(2000), 100);

cuboidRoute(25000) should return 320.

assert.strictEqual(cuboidRoute(25000), 320);

cuboidRoute(500000) should return 1309.

assert.strictEqual(cuboidRoute(500000), 1309);

cuboidRoute(1000000) should return 1818.

assert.strictEqual(cuboidRoute(1000000), 1818);

--seed--

--seed-contents--

function cuboidRoute(n) {

  return true;
}

cuboidRoute(2000);

--solutions--

function cuboidRoute(n) {
  // Based on https://www.mathblog.dk/project-euler-86-shortest-path-cuboid/
  function getLength(a, b) {
    return Math.sqrt(a ** 2 + b ** 2);
  }

  let M = 2;
  let counter = 0;

  while (counter < n) {
    M++;
    for (let baseHeightWidth = 3; baseHeightWidth <= 2 * M; baseHeightWidth++) {
      const pathLength = getLength(M, baseHeightWidth);
      if (Number.isInteger(pathLength)) {
        if (baseHeightWidth <= M) {
          counter += Math.floor(baseHeightWidth / 2);
        } else {
          counter += 1 + M - Math.floor((baseHeightWidth + 1) / 2);
        }
      }
    }
  }

  return M;
}