1.8 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f4691000cf542c50ff7b | Problema 252: Fori convessi | 5 | 301900 | problem-252-convex-holes |
--description--
Dato un insieme di punti su un piano, definiamo un foro convesso come un poligono convesso avente come vertici uno dei punti indicati e non contenente nessuno dei punti indicati al suo interno (oltre ai vertici, altri punti indicati possono trovarsi sul perimetro del poligono).
Ad esempio, l'immagine sottostante mostra una serie di venti punti e alcuni di questi fori convessi. Il foro convesso mostrato come un ettagono rosso ha una superficie pari a 1049694.5 unità quadrate, che è la maggiore area possibile per un foro convesso sull'insieme di punti dato.
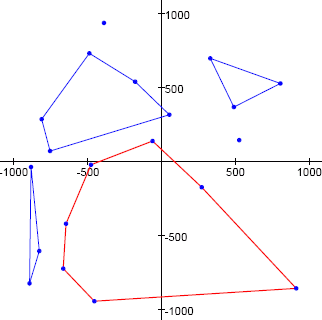
Per il nostro esempio, abbiamo usato i primi 20 punti (T_{2k − 1}, T_{2k}), per k = 1, 2, \ldots, 20, prodotto con il generatore di numeri pseudo-casuali:
$$\begin{align} S_0 & = 290\,797 \\ S_{n+1} & = {S_n}^2 \; \text{mod} \; 50\,515\,093 \\ T_n & = (S_n \; \text{mod} \; 2000) − 1000 \end{align}$$
cioè (527, 144), (−488, 732), (−454, −947), …
Qual è l'area massima per un foro convesso sul set contenente i primi 500 punti nella sequenza pseudo-casuale? Specifica la tua risposta includendo una cifra dopo il punto decimale.
--hints--
convexHoles() dovrebbe restituire 104924.
assert.strictEqual(convexHoles(), 104924);
--seed--
--seed-contents--
function convexHoles() {
return true;
}
convexHoles();
--solutions--
// solution required