2.2 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f4d91000cf542c50ffeb | Problema 363: Curve di Bézier | 5 | 302024 | problem-363-bzier-curves |
--description--
Una curva cubica di Bézier è definita da quattro punti: P_0, P_1, P_2 e P_3.
La curva è costruita come segue:
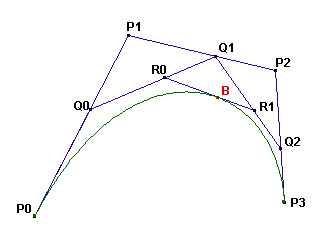
Sui segmenti P_0P_1, P_1P_2 e P_2P_3 i punti Q_0,$Q_1$ e Q_2 sono disegnati in modo tale che \frac{P_0Q_0}{P_0P_1} = \frac{P_1Q_1}{P_1P_2} = \frac{P_2Q_2}{P_2P_3} = t, con t in [0,1].
Sui segmenti Q_0Q_1 e Q_1Q_2 i punti R_0 e R_1 sono disegnati in modo tale che \frac{Q_0R_0}{Q_0Q_1} = \frac{Q_1R_1}{Q_1Q_2} = t per lo stesso valore di t.
Sul segmento R_0R_1 il punto B è disegnato in modo tale che \frac{R_0B}{R_0R_1} = t per lo stesso valore di t.
La curva di Bézier definita dai punti P_0, P_1, P_2, P_3 è il luogo di B tale che Q_0 prende tutte le posizioni possibili sul segmento P_0P_1. (Si noti che per tutti i punti il valore di t è lo stesso.)
Dalla costruzione è chiaro che la curva di Bézier sarà tangente ai segmenti P_0P_1 in P_0 e P_2P_3 in P_3.
Una curva cubica di Bézier con P_0 = (1, 0), P_1 = (1, v), P_2 = (v, 1) e P_3 = (0, 1) viene utilizzata per approssimare un quarto di cerchio. Il valore v > 0 è scelto in modo tale che l'area racchiusa tra le linee OP_0, OP_3 e la curva sia pari a \frac{π}{4} (l'area del quarto di circonferenza).
Di quanti punti percentuali la lunghezza della curva differisce dalla lunghezza del quarto di circonferenza? Cioè, se L è la lunghezza della curva, calcolare 100 × \displaystyle\frac{L − \frac{π}{2}}{\frac{π}{2}}. Dai la tua risposta approssimata a 10 cifre dopo il punto decimale.
--hints--
bezierCurves() dovrebbe restituire 0.0000372091.
assert.strictEqual(bezierCurves(), 0.0000372091);
--seed--
--seed-contents--
function bezierCurves() {
return true;
}
bezierCurves();
--solutions--
// solution required