1.4 KiB
1.4 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f5001000cf542c510012 | Problema 404: Ellissi incrociate | 5 | 302072 | problem-404-crisscross-ellipses |
--description--
E_a è un'ellisse con un'equazione della forma x^2 + 4y^2 = 4a^2.
E_a' è l'immagine rotata di E_a di θ gradi in senso antiorario attorno all'origine O(0, 0) per 0° < θ < 90°.
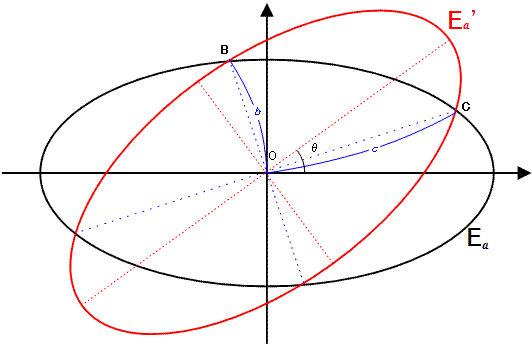
b è la distanza dall'origine dei due punti di intersezione più vicini all'origine e c è la distanza degli altri due punti di intersezione.
Chiamiamo una tripletta ordinata (a, b, c) una tripletta canonica ellissoidale se a, b, e c sono numeri interi positivi.
Per esempio, (209, 247, 286) è una tripletta ellissoidale canonica.
Sia C(N) il numero di triplette ellissoidali canoniche distinte (a, b, c) per a ≤ N.
Si può verificare che C({10}^3) = 7, C({10}^4) = 106 e C({10}^6) = 11\\,845.
Trova C({10}^{17}).
--hints--
crisscrossEllipses() dovrebbe restituire 1199215615081353.
assert.strictEqual(crisscrossEllipses(), 1199215615081353);
--seed--
--seed-contents--
function crisscrossEllipses() {
return true;
}
crisscrossEllipses();
--solutions--
// solution required