1.5 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f4761000cf542c50ff88 | Problema 265: Círculos binários | 5 | 301914 | problem-265-binary-circles |
--description--
Os algarismos binários 2^N podem ser colocados em um círculo de modo que todas as subsequências de N algarismos no sentido horário sejam distintas.
Para N = 3, dois arranjos circulares são possíveis, ignorando rotações:
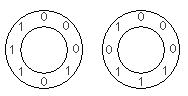
Para o primeiro arranjo, as subsequências de 3 algarismos, no sentido horário, são: 000, 001, 010, 101, 011, 111, 110 e 100.
Cada arranjo circular pode ser codificado como um número, concatenando os algarismos binários, começando com a subsequência de todos os zeros, como os bits mais significativos e prosseguindo no sentido horário. Os dois arranjos para N = 3 são, portanto, representados como 23 e 29:
$${00010111}_2 = 23\\ {00011101}_2 = 29$$
Chamando S(N) de soma das representações numéricas únicas, podemos ver que S(3) = 23 + 29 = 52.
Encontre S(5).
--hints--
binaryCircles() deve retornar 209110240768.
assert.strictEqual(binaryCircles(), 209110240768);
--seed--
--seed-contents--
function binaryCircles() {
return true;
}
binaryCircles();
--solutions--
// solution required