1.4 KiB
1.4 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f5081000cf542c510019 | Problema 411: Caminhos ladeira acima | 5 | 302080 | problem-411-uphill-paths |
--description--
Considere n um inteiro positivo. Suponha que haja estações nas coordenadas (x, y) = (2^i\bmod n, 3^i\bmod n) para 0 ≤ i ≤ 2n. Consideraremos estações com as mesmas coordenadas que a mesma estação.
Queremos formar um caminho de (0, 0) a (n, n) de modo que as coordenadas x e y nunca diminuam.
Considere S(n) como o número máximo de estações pelas quais um caminho pode passar.
Por exemplo, se n = 22, existem 11 estações distintas, e um caminho válido pode passar por, no máximo, 5 estações. Portanto, S(22) = 5. O caso é ilustrado abaixo, com um exemplo de caminho ideal:
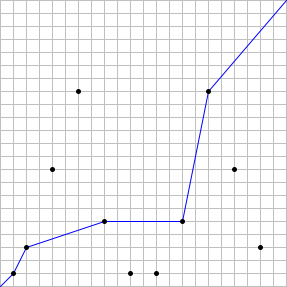
Também pode ser verificado que S(123) = 14 e S(10.000) = 48.
Encontre a \sum S(k^5) para 1 ≤ k ≤ 30.
--hints--
uphillPaths() deve retornar 9936352.
assert.strictEqual(uphillPaths(), 9936352);
--seed--
--seed-contents--
function uphillPaths() {
return true;
}
uphillPaths();
--solutions--
// solution required