1.7 KiB
1.7 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f5191000cf542c51002b | Problema 428: Colar de círculos | 5 | 302098 | problem-428-necklace-of-circles |
--description--
Considere a, b e c números positivos.
Considere W, X, Y, Z como quatro pontos colineares, onde |WX| = a, |XY| = b, |YZ| = c e |WZ| = a + b + c.
Considere C_{\text{in}} como o círculo com o diâmetro XY.
Considere C_{\text{out}} como o círculo com o diâmetro WZ.
O trio (a, b, c) é chamado de trio do colar se você puder dispor k ≥ 3 círculos distintos C_1, C_2, \ldots, C_k, tais que:
C_inão tem pontos interiores em comum com qualquerC_jpara1 ≤ i,j ≤ kei ≠ j,C_ié tangente tanto aC_{\text{in}}quanto aC_{\text{out}}para1 ≤ i ≤ k,C_ié tangente aC_{i + 1}para1 ≤ i < k, eC_ké tangente aC_1.
Por exemplo, (5, 5, 5) e (4, 3, 21) são trios do colar, enquanto é possível mostrar que (2, 2, 5) não é.
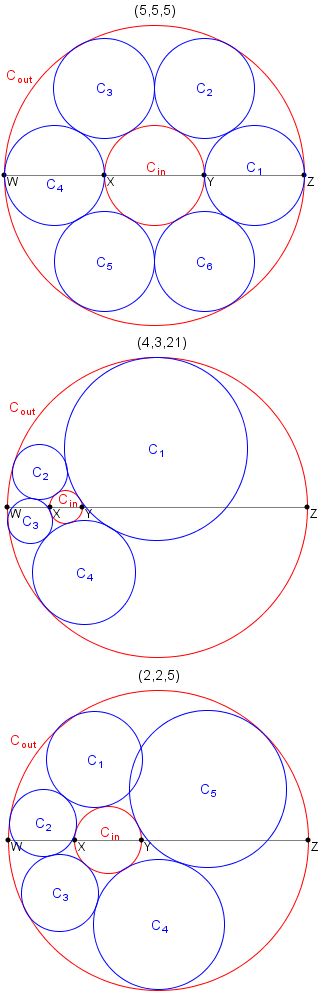
Considere T(n) como o número de trios de colar (a, b, c), tal que a, b e c sejam inteiros positivos e b ≤ n. Por exemplo, T(1) = 9, T(20) = 732 and T(3.000) = 438.106.
Encontre T(1.000.000.000).
--hints--
necklace(1000000000) deve retornar 747215561862.
assert.strictEqual(necklace(1000000000), 747215561862);
--seed--
--seed-contents--
function necklace(n) {
return true;
}
necklace(1000000000)
--solutions--
// solution required