2.0 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f5451000cf542c510057 | Problema 472: Distância confortável II | 5 | 302149 | problem-472-comfortable-distance-ii |
--description--
Existem N assentos em uma fila. N pessoas vêm umas atrás das outras para preencher os lugares de acordo com as seguintes regras:
- Nenhuma pessoa se senta ao lado de outra.
- A primeira pessoa escolhe qualquer assento.
- Cada pessoa subsequente escolhe o assento mais distante de qualquer outra pessoa já sentada, desde que não viole a regra 1. Se houver mais de uma escolha satisfazendo esta condição, então a pessoa escolhe a mais à esquerda.
Observe que, devido à regra 1, alguns lugares certamente ficarão sem ocupação, e que o número máximo de pessoas que podem estar sentadas é menor que N (para N > 1).
Aqui estão os possíveis arranjos para N = 15:
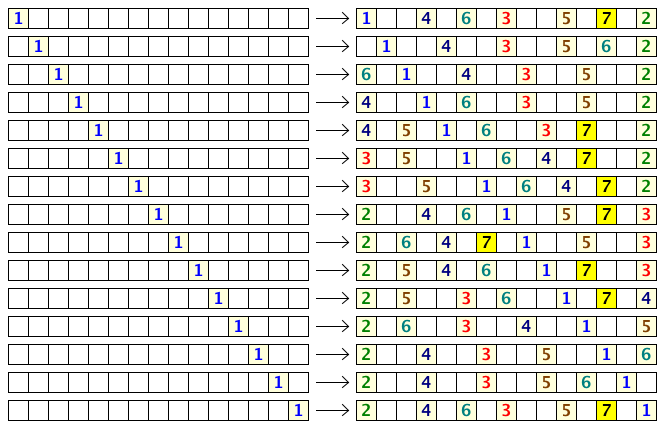
Vemos que, se a primeira pessoa escolher corretamente, os 15 assentos podem acomodar até 7 pessoas. Vemos também que a primeira pessoa tem 9 opções para maximizar o número de pessoas que podem se sentar.
Considere f(N) como o número de escolhas que a primeira pessoa tem de maximizar o número de ocupantes para N assentos em uma fila. Assim, f(1) = 1, f(15) = 9, f(20) = 6, e f(500) = 16.
Além disso, \sum f(N) = 83 para 1 ≤ N ≤ 20 e \sum f(N) = 13.343 para 1 ≤ N ≤ 500.
Encontre \sum f(N) para 1 ≤ N ≤ {10}^{12}. Dê os últimos 8 algarismos da sua resposta.
--hints--
comfortableDistanceTwo() deve retornar 73811586.
assert.strictEqual(comfortableDistanceTwo(), 73811586);
--seed--
--seed-contents--
function comfortableDistanceTwo() {
return true;
}
comfortableDistanceTwo();
--solutions--
// solution required