3.0 KiB
id, title, challengeType, forumTopicId, dashedName
| id | title | challengeType | forumTopicId | dashedName |
|---|---|---|---|---|
| 5900f4031000cf542c50ff15 | Завдання 150. Пошук трикутного масиву для меншого трикутника з мінімальною сумою | 5 | 301781 | problem-150-searching-a-triangular-array-for-a-sub-triangle-having-minimum-sum |
--description--
У трикутному масиві цілих додатних і від'ємних чисел ми хочемо знайти такий менший трикутник, сума чисел у якому була б найменшою.
У наведеному нижче прикладі можна легко перевірити, чи задовільняє виділений трикутник цій умові, маючи суму −42.
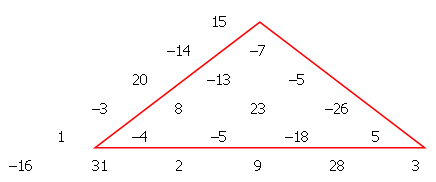
Ми хочемо створити такий трикутний масив з тисячею рядків, тому ми генеруємо 500500 псевдовипадкових чисел s_k у діапазоні ±2^{19}, використовуючи тип генератора випадкових чисел (відомий як лінійний конгруентний метод) наступним чином:
$$\begin{align} t := & \ 0\\ \text{for}\ & k = 1\ \text{up to}\ k = 500500:\\ & t := (615949 × t + 797807)\ \text{modulo}\ 2^{20}\\ & s_k := t − 219\\ \end{align}$$
Таким чином: s_1 = 273519, s_2 = −153582, s_3 = 450905 і т. д.
Трикутний масив утворений з використанням псевдовипадкових чисел:
$$ s_1 \\ s_2\;s_3 \\ s_4\; s_5\; s_6 \\ s_7\; s_8\; s_9\; s_{10} \\ \ldots $$
Менші трикутники можуть починатися з будь-якого елемента масиву і сягати вниз як завгодно далеко (захоплюючи два елементи безпосередньо під ним з наступного ряду, три елементи безпосередньо під ним з наступного ряду і так далі).
"Сума меншого трикутника" визначається як сума всіх чисел, які він містить.
Знайдіть найменшу можливу суму меншого трикутника.
--hints--
smallestSubTriangleSum() має повернути -271248680.
assert.strictEqual(smallestSubTriangleSum(), -271248680);
--seed--
--seed-contents--
function smallestSubTriangleSum() {
return true;
}
smallestSubTriangleSum();
--solutions--
// solution required